Lab 11: Part 2A: Recursive Turtles
The turtle section of our quick-reference page
has information about the available turtle and turtleBeads drawing
commands.
The Turtle module
API is the official
Python documentation for the turtle module.
Setup
In the lab11 folder, open recursiveTurtles.py.
At the bottom of the starter file is a function run, which invokes
setupTurtle. The invocations of the functions you write (e.g., row())
will go inside run(). This is how you will test your turtle functions today.
Task 1. The provided square function and how to test
def square(length):
"""Draws a square of size length maintains heading
and position invariant"""
for _ in range(4):
fd(length)
lt(90)# WRITE YOUR FUNCTIONS HERE
...then invoke square in the run function.
How to test your functions:
- Call your function from within the
runfunction (near the bottom of your file) - Run your file in Thonny
- This will automatically call the
runfunction, which in turn will call your function.
Do a test run with square by calling square from within run.
Note that there is a test_recursiveTurtles.py file in your lab09
folder, but it does not include tests for all the functions and the
tests rely on drawing lines in a certain order, which you do not
necessarily have to follow. So, for today, it is better to test by calling your
functions from within the run function.
Task 2: Row of squares
Write a recursive method called row(number, size) that draws a horizontal row of number squares of size size.
This function must be recursive and maintain a position and heading invariant.
FYI: In the example screenshots below, the Turtle's pen was set to red ( via pencolor('red')), but your pen color will be black by default.
row(3, 50)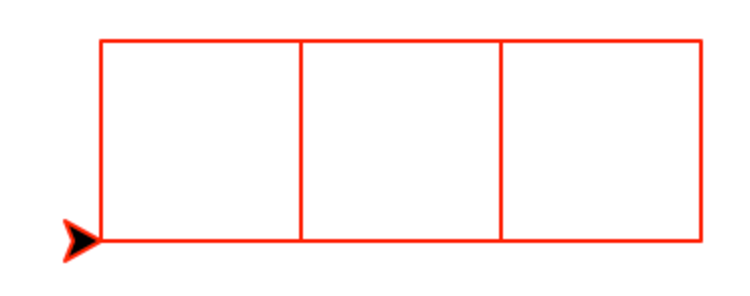
|
row(5,25)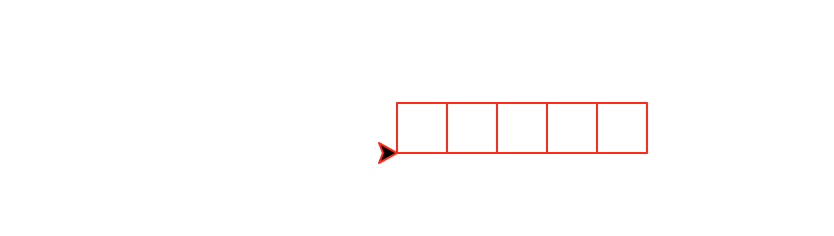
|
Task 3: Spaced row of squares
Write a recursive method called spacedRow(number, size) that draws a horizontal row of number squares of size size with a constant space of size/4 between each square.
This function must be recursive and maintain a position and heading invariant.
spacedRow(3,50)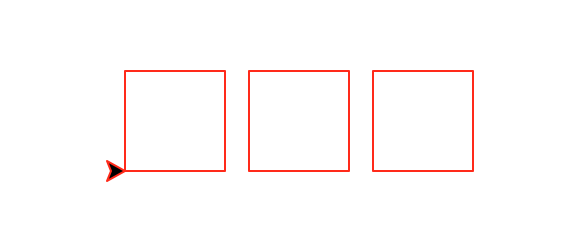
|
spacedRow(5,25)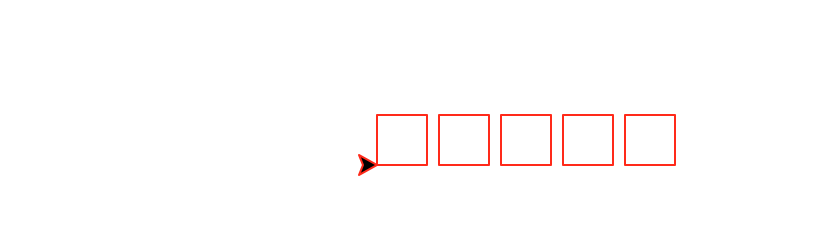
|
Task 4: Decreasing row of squares
Write a recursive method called decreasingRow(number,size) that draws a horizontal row of number squares. The first square has size size and each subsequent square is half the size of the previous one.
This function must be recursive and maintain a position and heading invariant.
decreasingRow(3,100)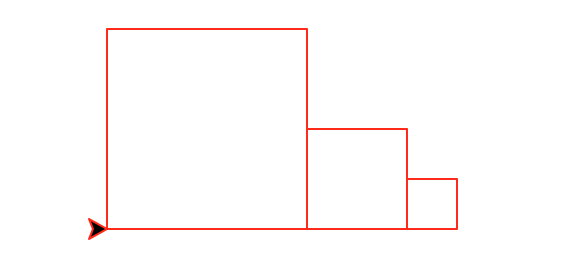
|
decreasingRow(5,100)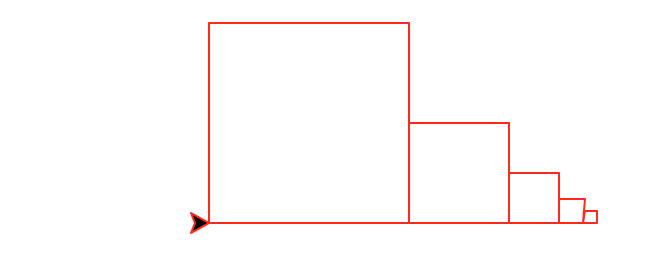
|
Task 5: Nested squares
Write a recursive method called nestedSquares(number,size) that draws number nested squares. The largest square has size size and each subsequent square is half the size of the previous one. The squares are anchored in the lower left corner.
This function must be recursive and maintain a position and heading invariant.
nestedSquares(3,90)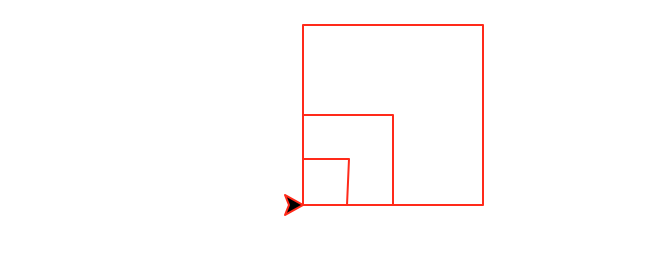
|
nestedSquares(5,130)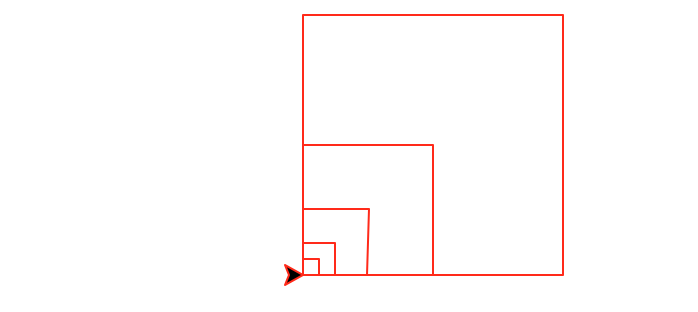
|
Task 6: Diagonal squares
Write a recursive method called diagonal(number,size) that draws number decreasing diagonal squares. The largest square has size size and each subsequent square is half the size of the previous one.
This function must be recursive and maintain a position and heading invariant.
diagonal(1,100)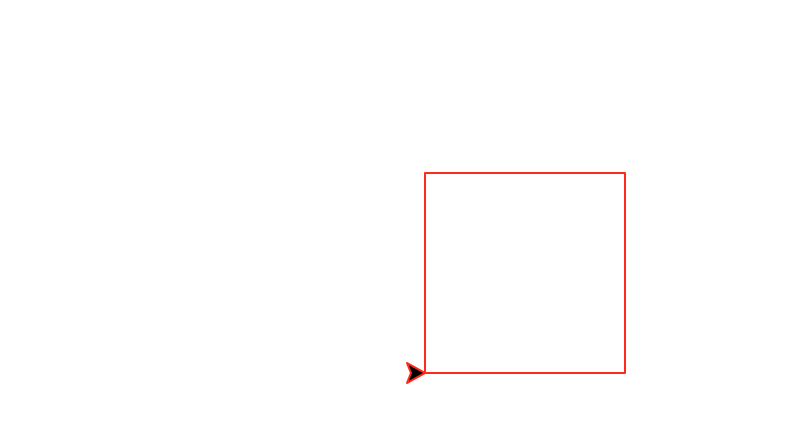
|
diagonal(2,100)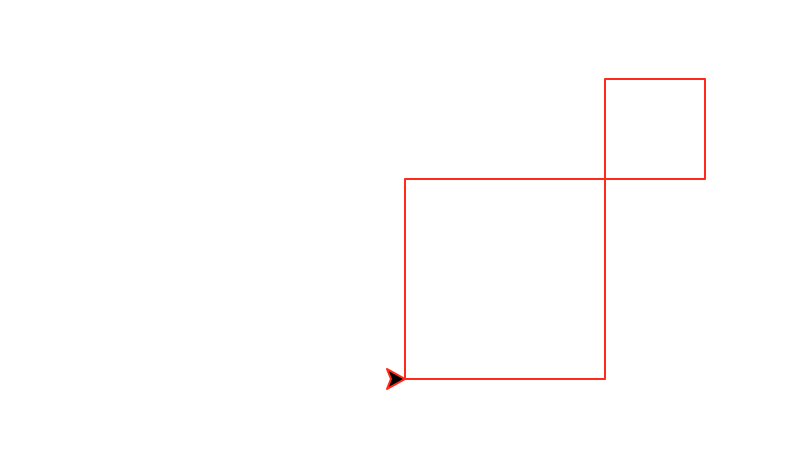
|
diagonal(3,100)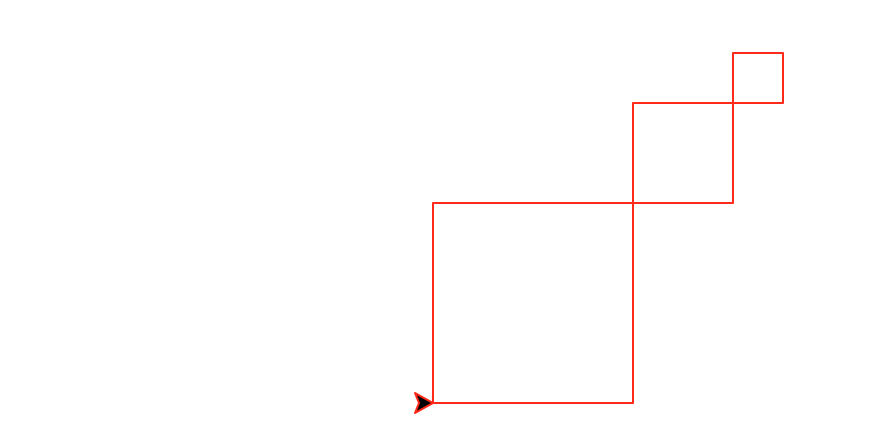
|
Task 7: Double Diagonal squares
Write a recursive method called doubleDiagonal(number,size) that draws number decreasing diagonal squares. The largest square has size size and each subsequent square is half the size of the previous one. Each recursive call draws two new squares: one anchored at the upper right corner and the other anchored at the lower left corner.
This function must be recursive and maintain a position and heading invariant.
doubleDiagonal(1,100)
|
doubleDiagonal(2,100)
|
doubleDiagonal(3,100)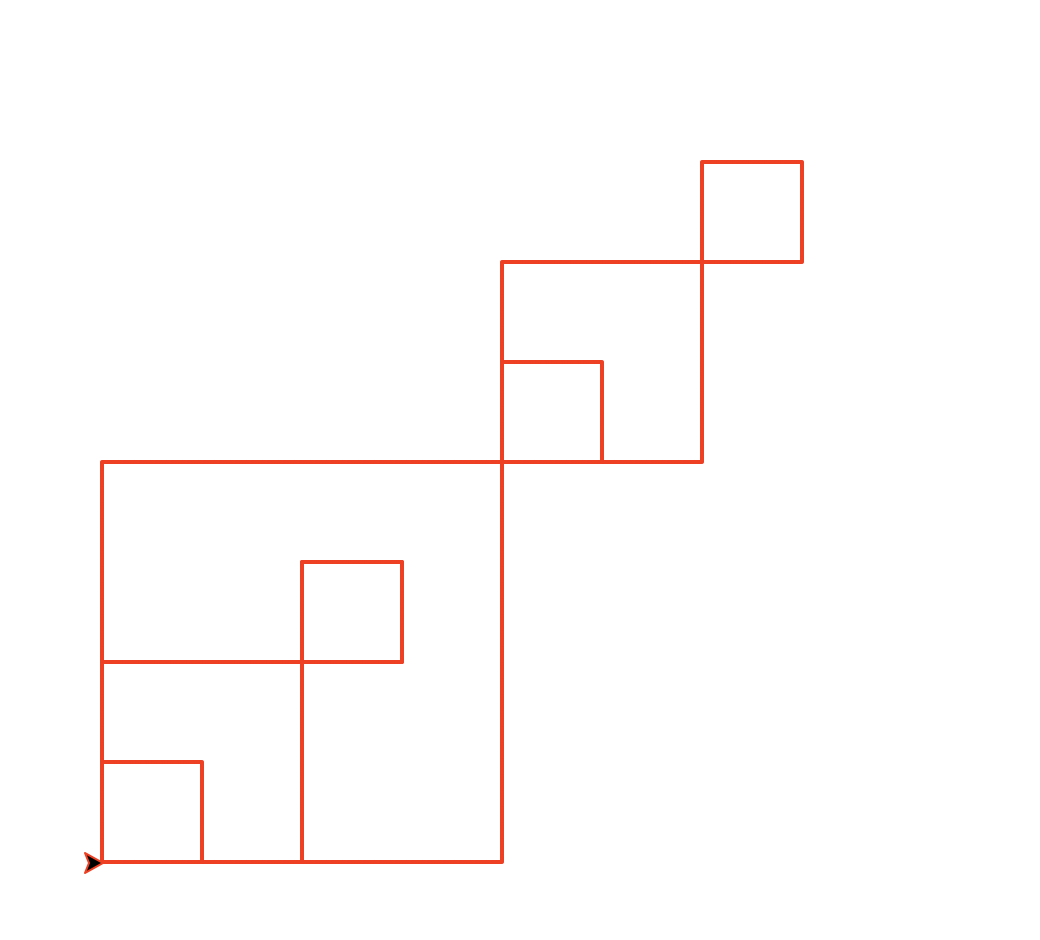
|
doubleDiagonal(4,100)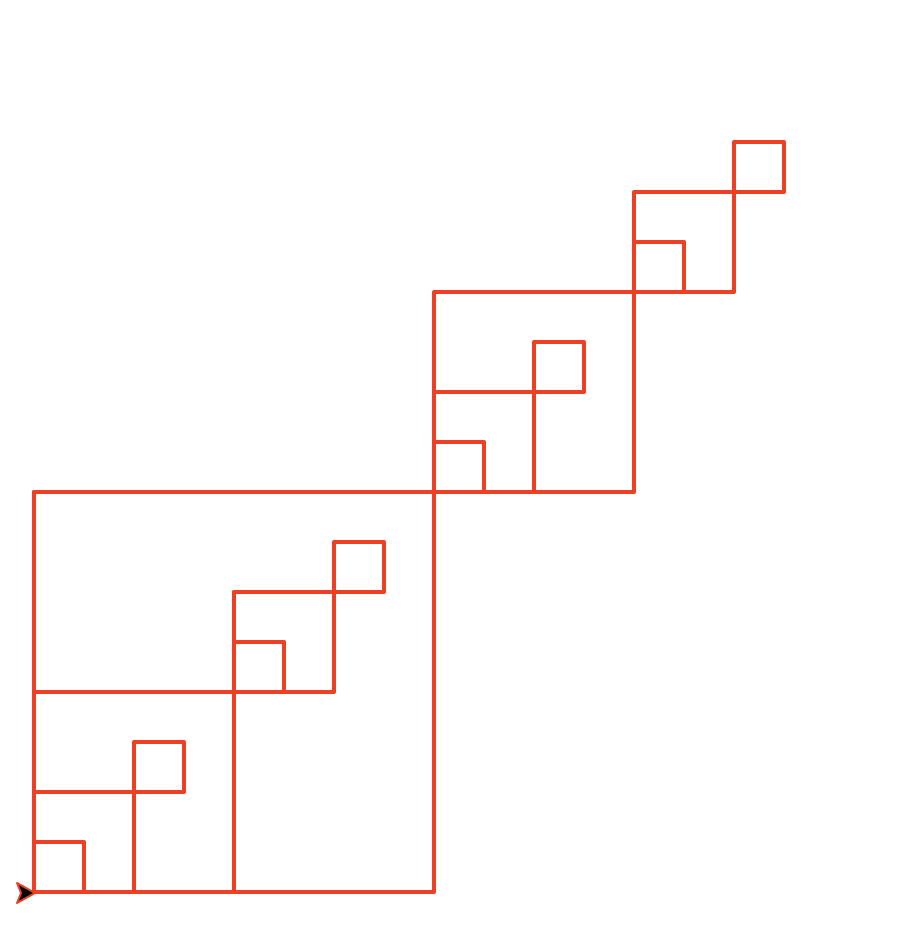
|
Task 8: Super diagonal squares
Write a recursive method called superDiagonal(number,size) that draws number decreasing diagonal squares. The largest square has size size and each subsequent square is half the size of the previous one. In superDiagonal, squares are placed on the diagonal at both the upper right corner and the lower left corner. Note: superDiagonal will not invoke diagonal.
This function must be recursive and maintain a position and heading invariant.
superDiagonal(1,125)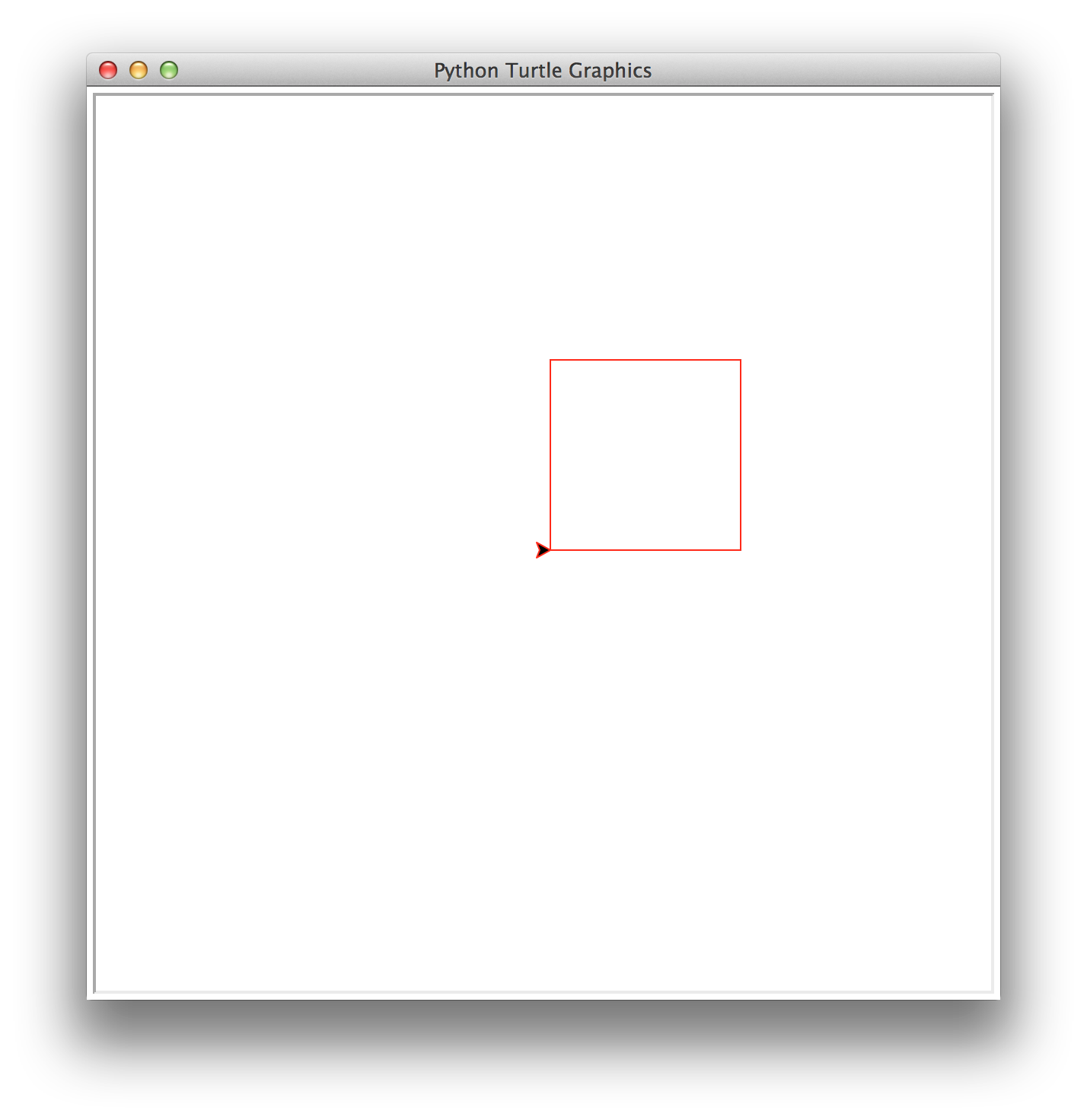
|
superDiagonal(2,125)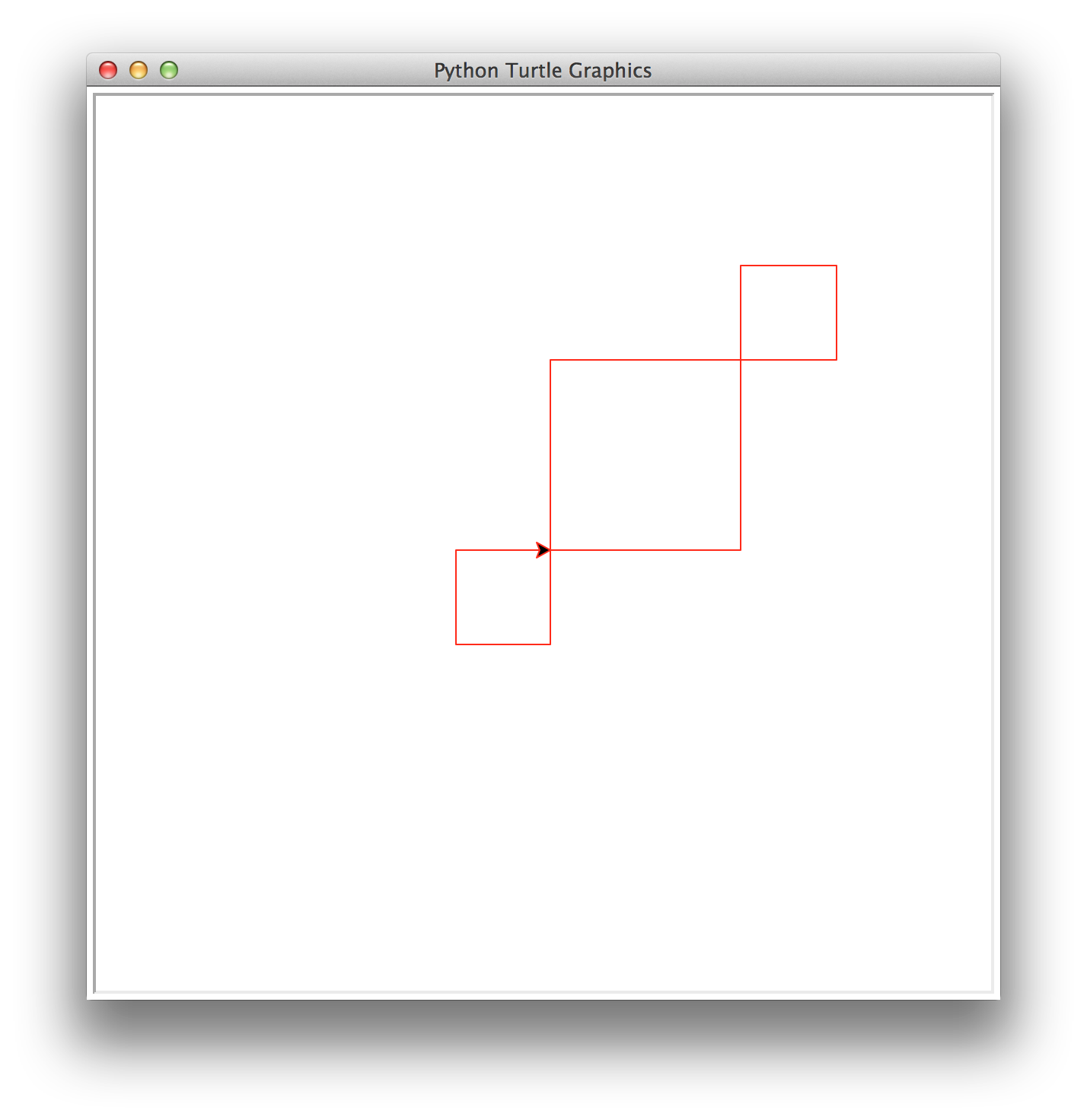
|
superDiagonal(3,125)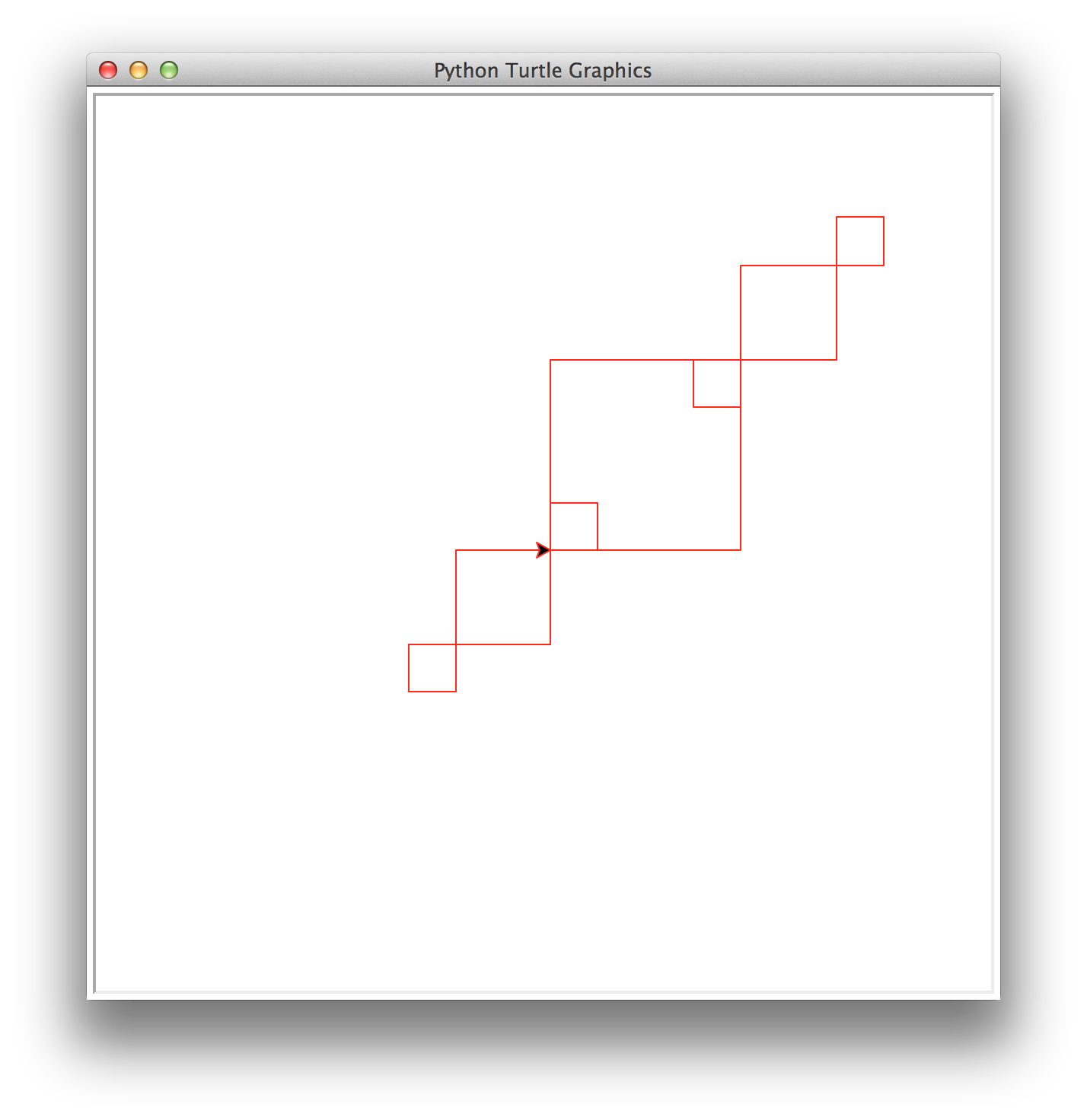
|
superDiagonal(4,125)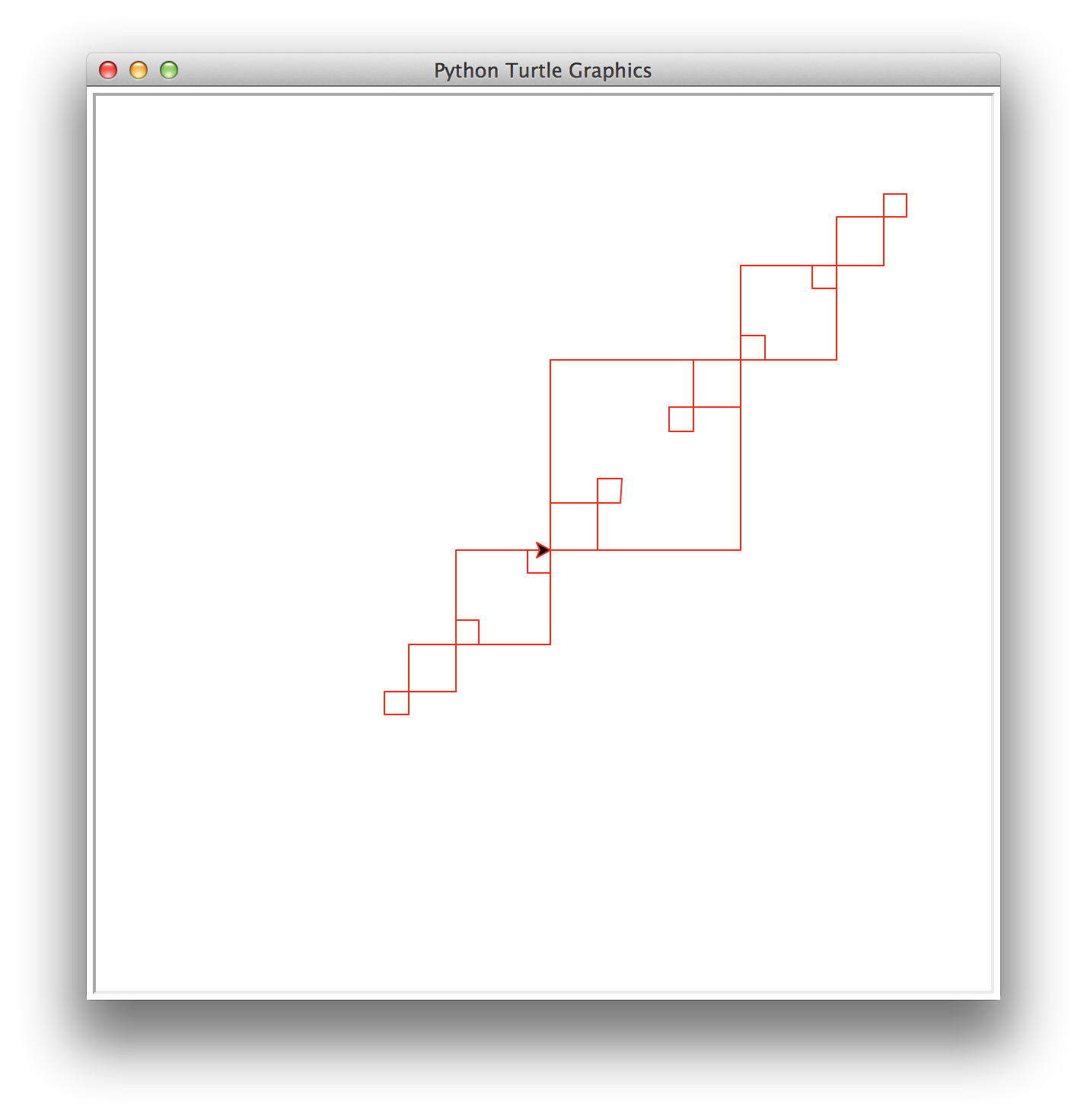
|
Table of Contents
- Lab 11 Home
- Part 1: Exercises (start with B notebook)
- Part 2A: Recursive Turtles (work on this part OR the next one)
- Part 2B: Recursive Drums (work on this part OR the previous one)
- Reference: Case-by-case recursion strategy
- Reference: Recursive design patterns
- Knowledge Check