Lab Reference - Recursion Design Patterns

This reference page contains examples of common recursive design patterns in CS111. These patterns share some common steps:

1. Some action to produce the fundamental unit of the design (e.g., one line of output; one shape in a visual pattern; one note in a song).
2. Recursion - an invocation of the same function that we're working on to repeat the design.

For turtle drawing functions, we may also have:

3. Setup - The movement of the turtle to get into position for what's next.
4. An invariant-preserving movement to get back to the starting position for each piece of the drawing.

Every recursive design we’re creating can be broken down into some combination of these steps. Understanding this can be useful, because it gives you some scaffolding to work with when you approach a new problem. These pieces of recursive designs can also be expressed along with other fundamental design questions that you should answer before you start working on a solution:

• What is the base case?
• What is the fundamental action?
• How many times will it recurse (both in total, and per function call frame)?
• Is setup needed? (only for turtle drawing, usually)
• Is there an invariant to preserve?

The rest of this page contains examples of recursive patterns you've seen. For each pattern, the corresponding design pattern is shown.

Act-recurse Patterns

These patterns have a simple act-recurse structure. Examples include:

def countDown(n):
    if n <= 0: # Base case
        pass
    else:
        # Act
        print(n)

        # Recurse
        countDown(n-1)

Output:

>>> countDown(5)
5
4
3
2
1

def tower(name):
    if len(name) == 0:  # Base case
        pass
    else:
        # Act
        print(name)

        # Recurse
        tower(name[1:])

Output:

>>> tower('Wellesley')
Wellesley
ellesley
llesley
lesley
esley
sley
ley
ey
y

Drawing nested squares also fits the act-recurse pattern:

def nestedSquares(num, size):
    if (number > 0):
        square(size) # action
        nestedSquares(num-1, size/2) # recursive call

Result:

>>> nestedSquares(3, 90)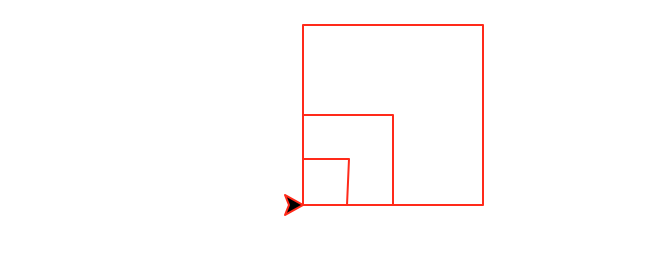

Act-recurse-act Patterns

These patterns take action both before and after the recursion. It's a bit hard to think through at first, but the two actions are actually sandwiched on either side of a lot of other actions when the recursion gets going.

def countDownUp(n):
    if n <= 0: # Base case
        pass
    else:
        # Act
        print(n)

        # Recurse
        countDownUp(n-1)

        # Act
        print(n)

Output:

>>> countDownUp(3)
3
2
1
1
2
3

Act-setup-recurse and Act-setup-recurse-invariant Patterns

These patterns involve some setup code before the next recursive call, and may involve an invariant (we usually require one).

def spiral(length, segments):
    if segments > 0:
        fd(length) # act
        lt(90) # setup
        spiral(length * 0.75, segments - 1)

spiral(100, 8)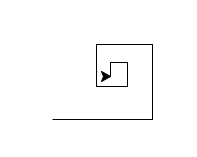

spiralReturn is the same pattern, but this time with code that enforces an invariant:

def spiralReturn(length, segments):
    if segments > 0:
        fd(length) # act
        lt(90) # setup
        spiralReturn(length * 0.75, segments - 1)
        lt(-90) # invariant
        bk(length) # invariant part 2

spiralReturn(100, 8)

Complex patterns

More complex patterns are possible. For example, from this lab, superDiagonal uses act-setup-recurse-setup-recurse-invariant:

def superDiagonal(number, size):
    '''
    Recursively draw a row of squares that get progressively smaller by
    1/2 each time where each successive square is anchored on the upper
    right corner of the previous square and the upper left corner of the
    previous square.
    '''
    if (number > 0):

        square(size)
        # back at lower left starting point
        # get into position for recursive call
        fd(size)
        lt(90)
        fd(size)
        rt(90)
        # recursive call for diagonal stemming from upper right corner
        # Note the 2. allows for more precision, e.g. if size is odd
        # then we get a more accurate half size.
        superDiagonal(number-1, size/2) #  first recursive call
        # maintain position invariant by undoing the steps before
        # the recursive call
        lt(90)
        bk(size)
        rt(90)
        bk(size)
        # back at lower left corner, facing East
        # draw the diagonal in the SouthWest direction
        lt(180)
        superDiagonal(number-1, size/2) # second recursive call
        rt(180)

>>> superDiagonal(3, 125)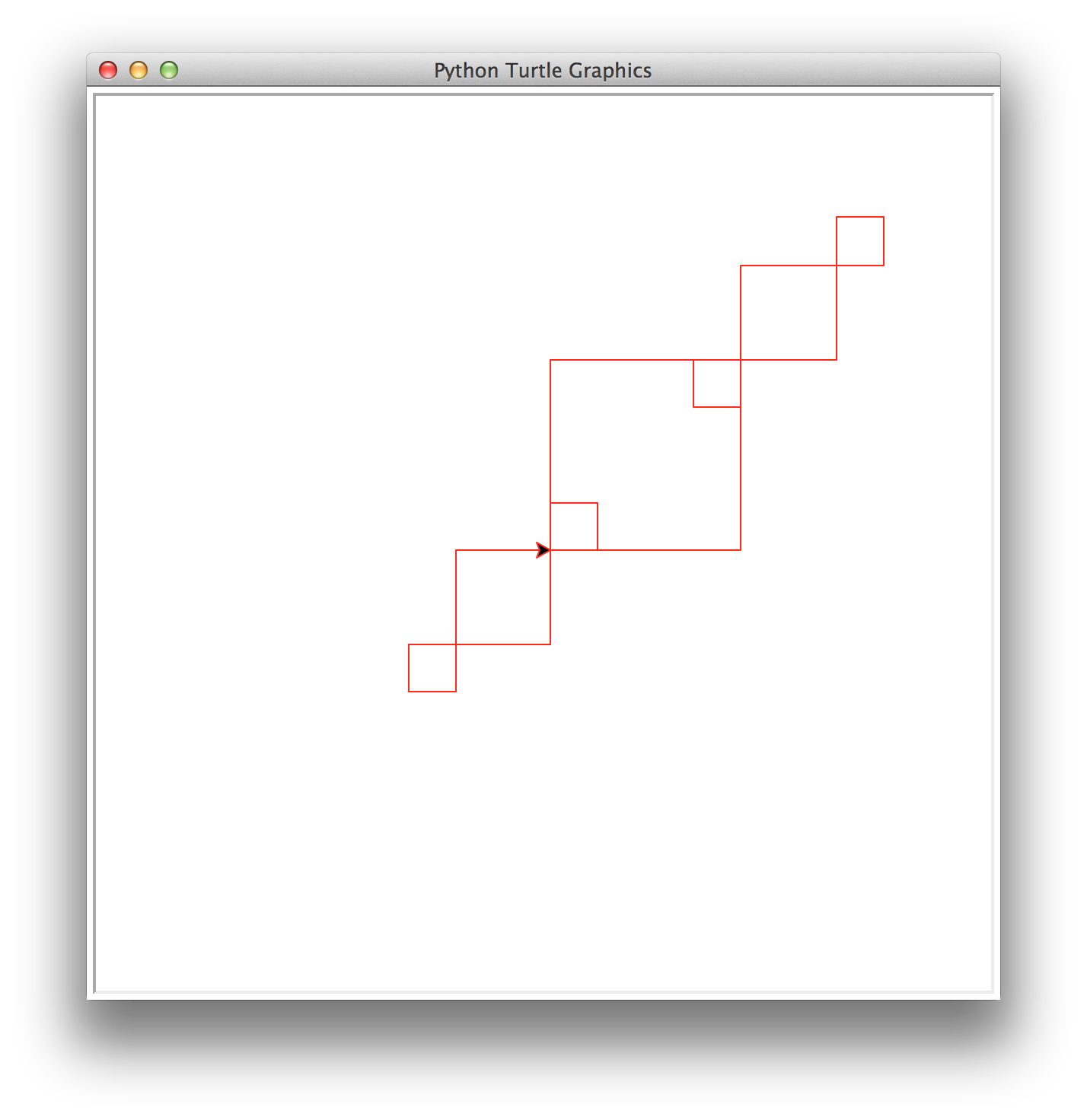

Meanwhile, triangleBeats uses recurse-act-recurse:

def triangleBeats(duration, complexity):
    """
    Adds a pattern of shorter and longer beats to the current track, with
    the longest beat in the center of the track, and shorter beats to
    either side. A single beat of the given duration is added, but before
    and after that, two more triangleBeats patterns are added, each with
    3/4 of the original duration and one less complexity. When called
    with zero or negative complexity, nothing is added to the current
    track.
    """
    if complexity > 0:
        triangleBeats(duration*0.75, complexity - 1) # recurse
        addBeat(duration) # act
        triangleBeats(duration*0.75, complexity - 1) # recurse

Here is what the result sounds like for triangleBeats(0.16, 3); you can see the correct printed output below as well.

a 0.09s snare beat
and a 0.12s snare beat
and a 0.09s snare beat
and a 0.16s snare beat
and a 0.09s snare beat
and a 0.12s snare beat
and a 0.09s snare beat

Table of Contents

• Lab 11 Home
• Part 1: Exercises (start with B notebook)
• Part 2A: Recursive Turtles (work on this part OR the next one)
• Part 2B: Recursive Drums (work on this part OR the previous one)
• Reference: Case-by-case recursion strategy
• Reference: Recursive design patterns
• Knowledge Check