Lab 11: Fruitful recursion w/ Turtle graphics

Task 0. Consider a different approach for rows of boxes

We designed recursive Turtle functions that would draw a pattern a given number of times.

For example, when we invoked row(3, 50) it would draw 3 squares.

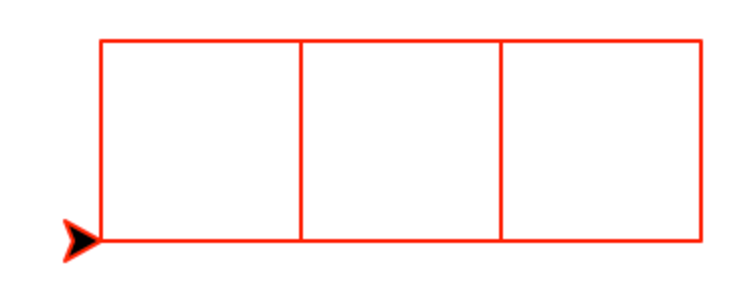
To make things more challenging, let's change it up a bit. We will tell the function the starting side length of the first square, and a shrink factor and a minimum side length that must be met in order for a square to be drawn. Consider the function newRow below:

def newRow(size, shrinkFactor, minimumSize):
    if size < minimumSize:
        pass
    else:
        square(size)
        fd(size)
        newRow(size*shrinkFactor, shrinkFactor, minimumSize)
        bk(size)

Here are two sample invocations of newRow:

newRow(size, shrinkFactor, minimumSize)

Example invocation 1:

newRow(50, 0.5, 20)

produces

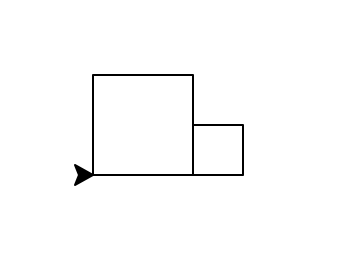
The first box has size 50, the second 25, and the third would be 12.5, but 12.5 < 20, so it stops.

Example invocation 2:

newRow(50, 0.8, 20)

produces

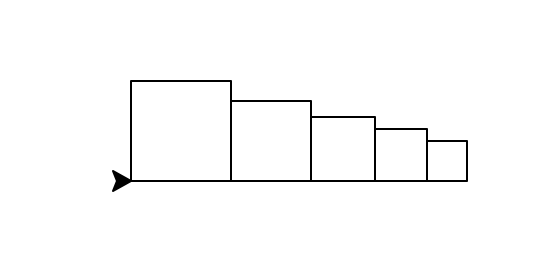
The box sides are 50, 40, 32, 25.6, and 20.48. The next one would be 16.38, but that is < 20, so it is not drawn.

Task 1. Write fruitfulRow

Using newRow (code above) as your starting point, write fruitfulRow so that the fruitful function returns the number of boxes that are drawn.

Example invocations of `fruitfulRow`:

In []: fruitfulRow(50, 0.5, 20)
Out[]: 2
In []: fruitfulRow(50, 0.8, 20)
Out[]: 5
In []: fruitfulRow(100, 0.75, 18)
Out[]: 6
In []: fruitfulRow(100, 0.9, 10)
Out[]: 22

Task 2. fruitfulRowImproved

In this next task, we want to create an improved version of the row function that instead of just returning a single value (squareCount) it returns a tuple indicating how many squares were drawn and the total distance travelled by the Turtle/cursor.

Capturing tuples returned from a function

In order to complete this task, study the following example that demonstrates a function that returns a tuple...

def pad(x, y, padding):
    return x + padding, y + padding

Given the above code, make predictions of what the following print statements would produce:

x, y = pad(300, 200, 10)
print(x) # ???
print(y) # ???

Run your code in Canopy to check your predictions. Note how the function pad returns a tuple. Because of this, we can capture its results in a tuple: x, y = pad(300, 200, 10).

Once you understand the above code, copy and complete the following fruitfulRowTuple function in your lab11/fruitfulTurtles.py file:

def fruitfulRowTuple(size, shrinkFactor, minimumSize):
    if size < minimumSize:
        return ???
    else:
        square(size)
        fd(size)
        ??? = 1 + fruitfulRowTuple(size*shrinkFactor, shrinkFactor, minimumSize)
        bk(size)
        return ???

Important observation about the above function: Note how the base case also needed to return a tuple, 0,0. It's essential that the value type returned by the base case is consistent with what is returned in the recursive case.