Lab 11: Extra Fruitful recursion w/ Turtle graphics

Task 1. nestedSquares

Write a fruitful recursive function called nestedSquares returns a drawing of nested squares as shown in the examples below.

Parameters:

The size (length) of the square to be drawn
The shrink factor of the successive squares to be drawn
The minimum sidelength of a square; boxes will only draw a square if the side is greater than this minimum sidelength
The color of the Turtle's pen

Before writing any code, skim through the following examples and read the hints that follow.

Example A.

nestedSquares(400, 0.2, 100, 'blue')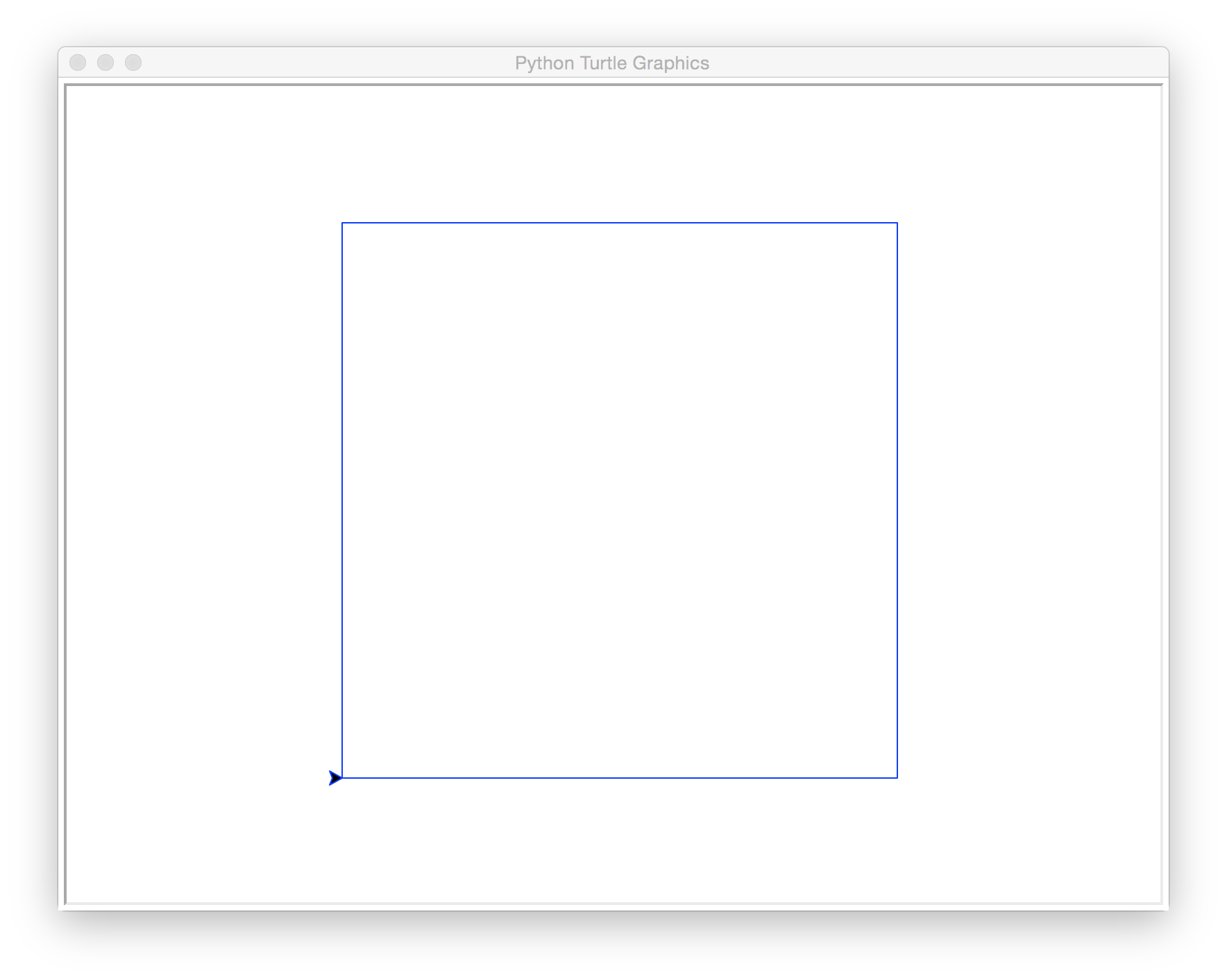

1 square, 1600 length (400 * 4 sides = 1600)

No more squares drawn because 400 * 0.2 = 80, and 80 is less than the min sidelength of 100.

Example B.

nestedSquares(400, 0.4, 100, 'magenta')

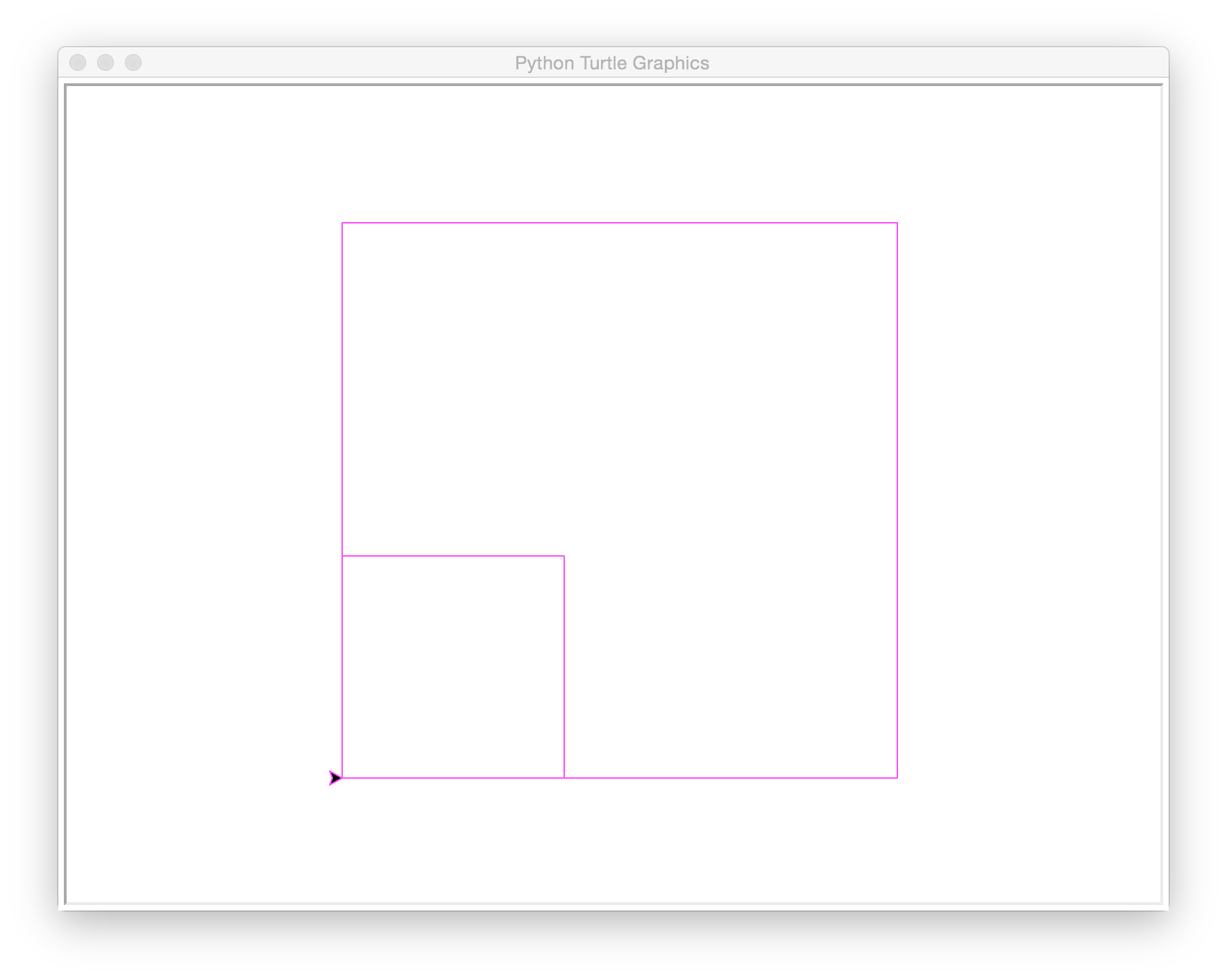
2 squares, 2240 total length

 1600 largest square (400 * 4 sides)
+ 640 small square (160 * 4 sides)
=====
 2240 total length

Example C.

nestedSquares(400, 0.75, 100, 'black')

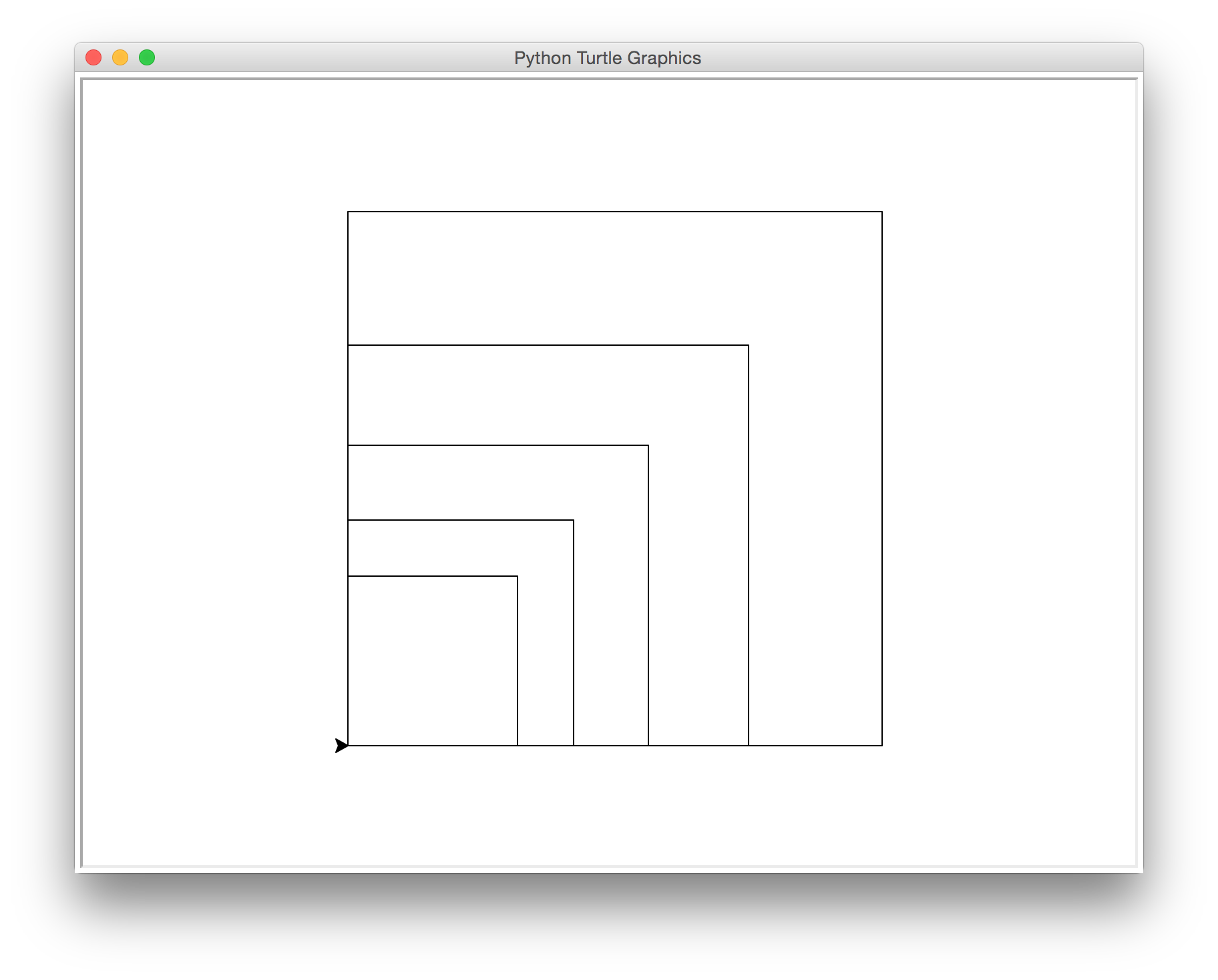
5 squares, 4881.25 total length

  1600   (400 * 4 sides)
+ 1200   (300 * 4 sides)
+ 900    (225 * 4 sides)
+ 675    (168.75 * 4 sides)
+ 506.25 (126.5625 * 4 sides)
=========
  4881.25 total length

Example D.

nestedSquares(100, 0.8, 20, 'red')

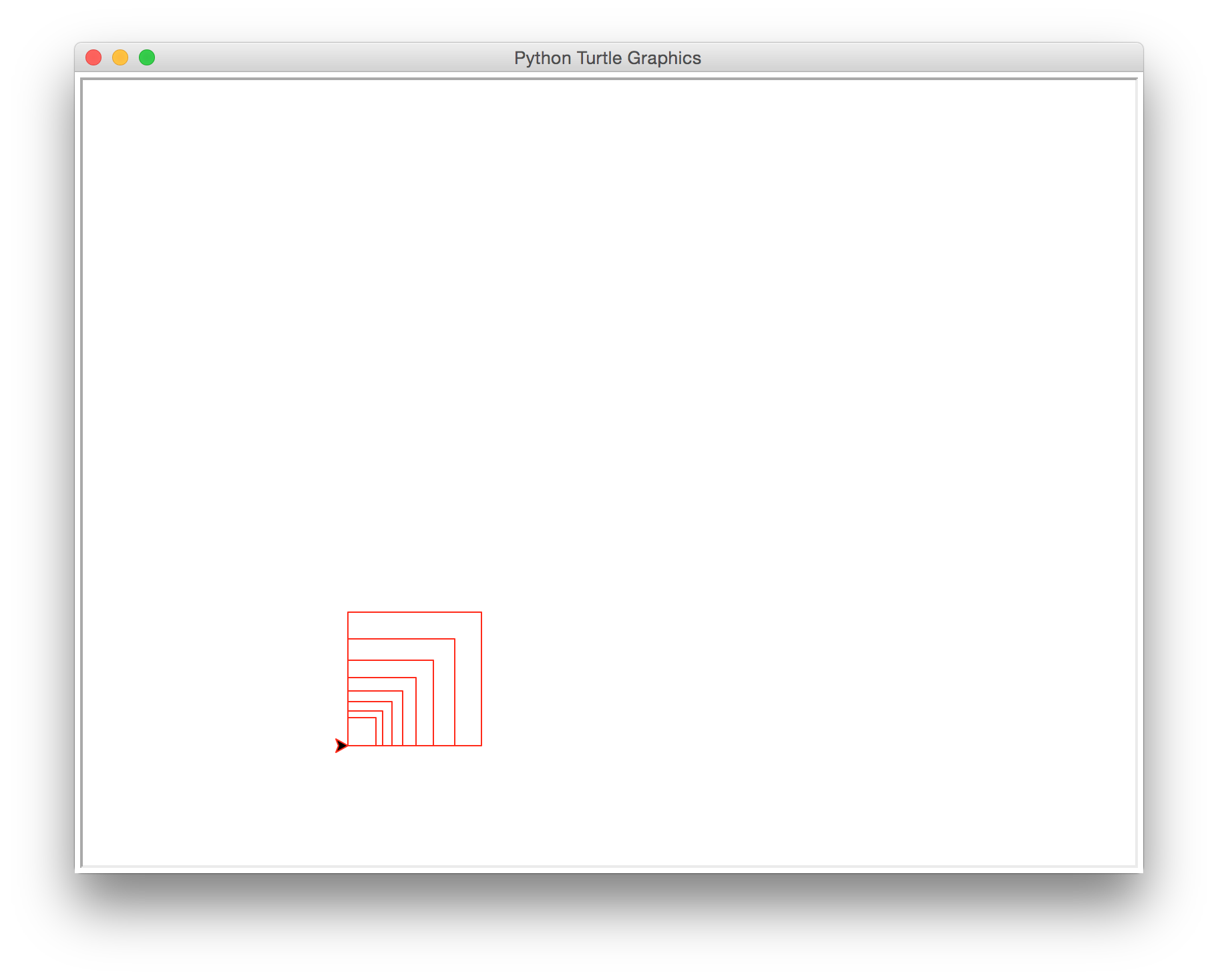
8 squares, 1664.45568 total length

  400       (100 * 4 sides)
+ 320       (80 * 4 sides)
+ 256       (64 * 4 sides)
+ 204.8     (51.2 * 4 sides)
+ 163.84    (40.96 * 4 sides)
+ 131.072   (32.768 * 4 sides)
+ 104.8576  (26.2144 * 4 sides)
+ 83.88608  (20.97152 * 4 sides)
===========
1,664.45568 total length

Hints

First, write the recursive function to produce the picture of nested squares. Relevant things to think about:
- When does the recursion end? Which parameter(s) determine if it is the base case?
- Handle the recursive case: draw one square and let recursion draw the remaining squares.
- Adjust the relevant parameters in the recursive call to ensure that the problem gets smaller each time.
After the above works, then add in the fruitful counting of squares only. You will need a variable to keep track of the square count, and you will need to return that value.
After the counting of squares works, then add the fruitful sum of all the lengths drawn. Each time the Turtle moves forward, keep track of that “mileage”.

There are hints in Helpful Hints and Diagrams (see Table of Contents below), in particular, this Turtle Hints diagram may be helpful.

Argh! My function doesn't work! Help!

Try some of these debugging tips:

Draw out the first few cases on paper, and make sure that you have broken down the problem correctly.

Additionally, add print statements at the start and end of your function to display each parameter value, e.g.

print("nestedSquares(" + str(size) + str(shrink) + ... + ")")

This also helps you trace the recursion as it unfurls.

Task 2. windows

Create a function called windows that produces the fruitful recursive square patterns shown below:

windows(64, 0.4, 20, 'magenta')

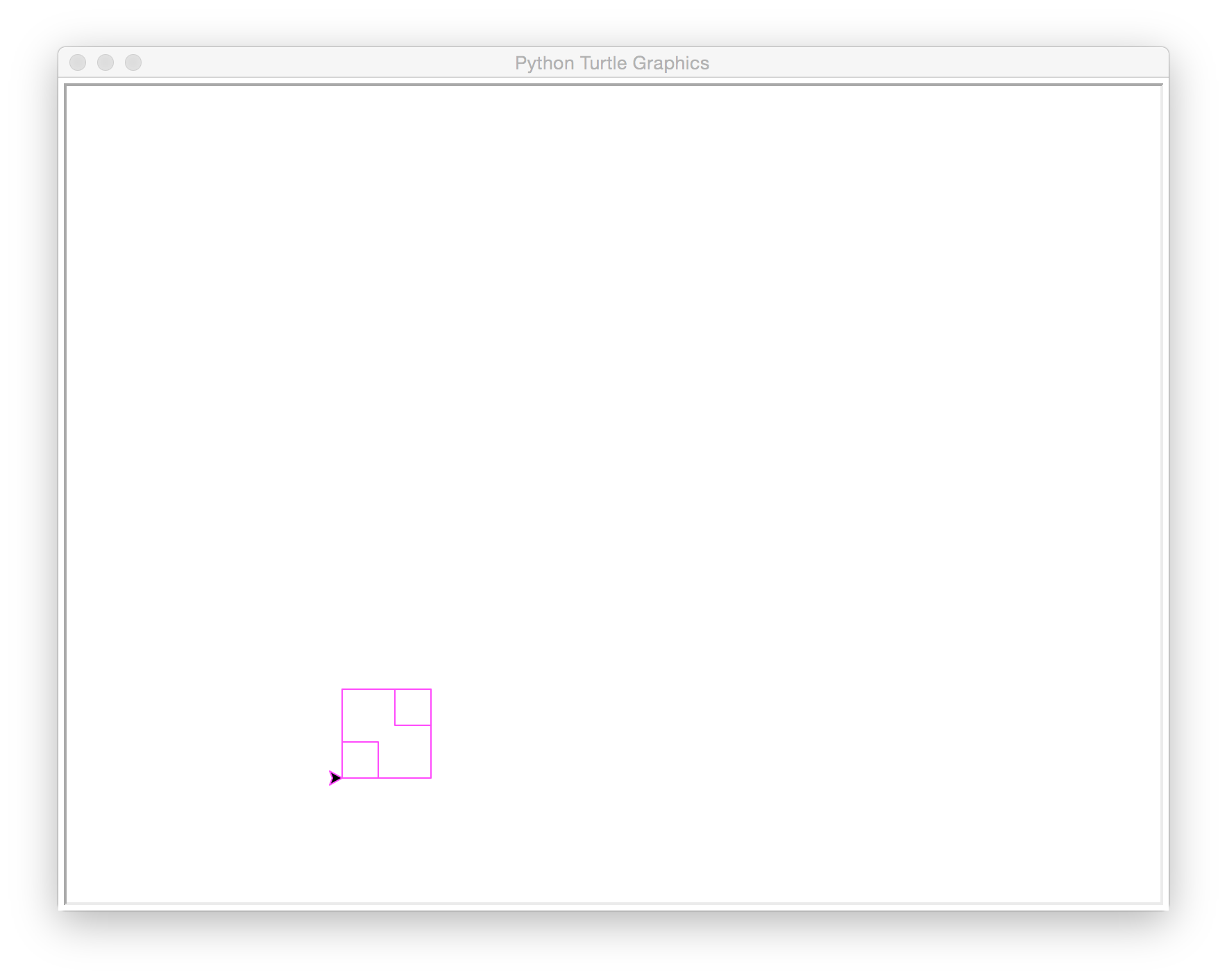
3 boxes drawn, 460.8 total length

  256   (64 * 4 sides)
+ 102.4 (25.6 * 4 sides)
+ 102.4 (25.6 * 4 sides)
=======
  460.8 total length

How to approach this design

Do not use a square helper function in this task— the squares in the pattern should be drawn as a side effect of moving the Turtle into position between recursive calls (as shown in the following video).

In order to do this, think of the fundamental piece of this design not as a single square, but as a corner of a square (repeated 2x via recursion to make a complete square).

Here's a video demonstrating this approach:

windows(160, 0.4, 20, 'orange')

More examples

Example B.

windows(160, 0.4, 20, 'magenta')

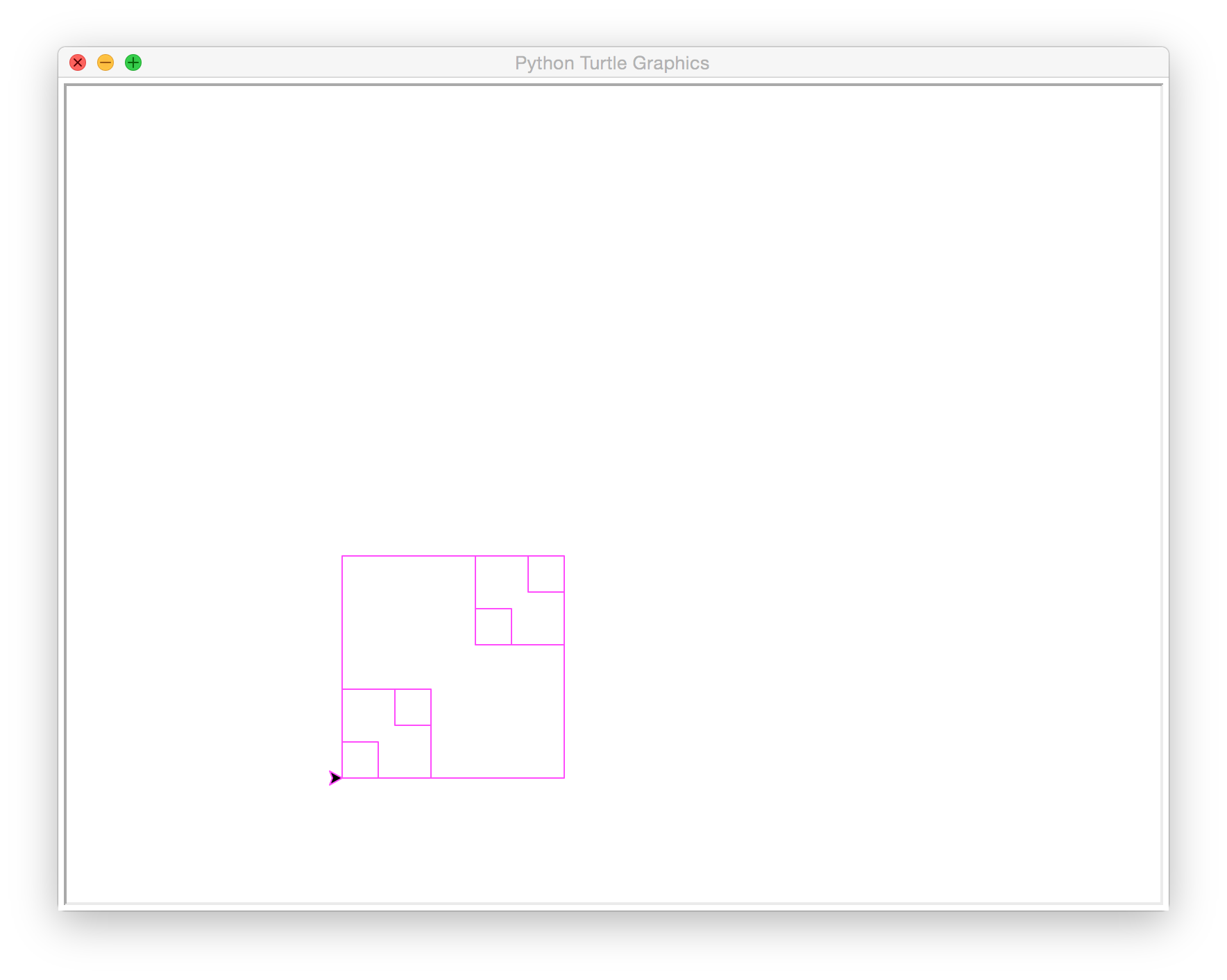
7 boxes drawn, 1561.6 total length

Example C.

windows(400, 0.4, 20, 'magenta')

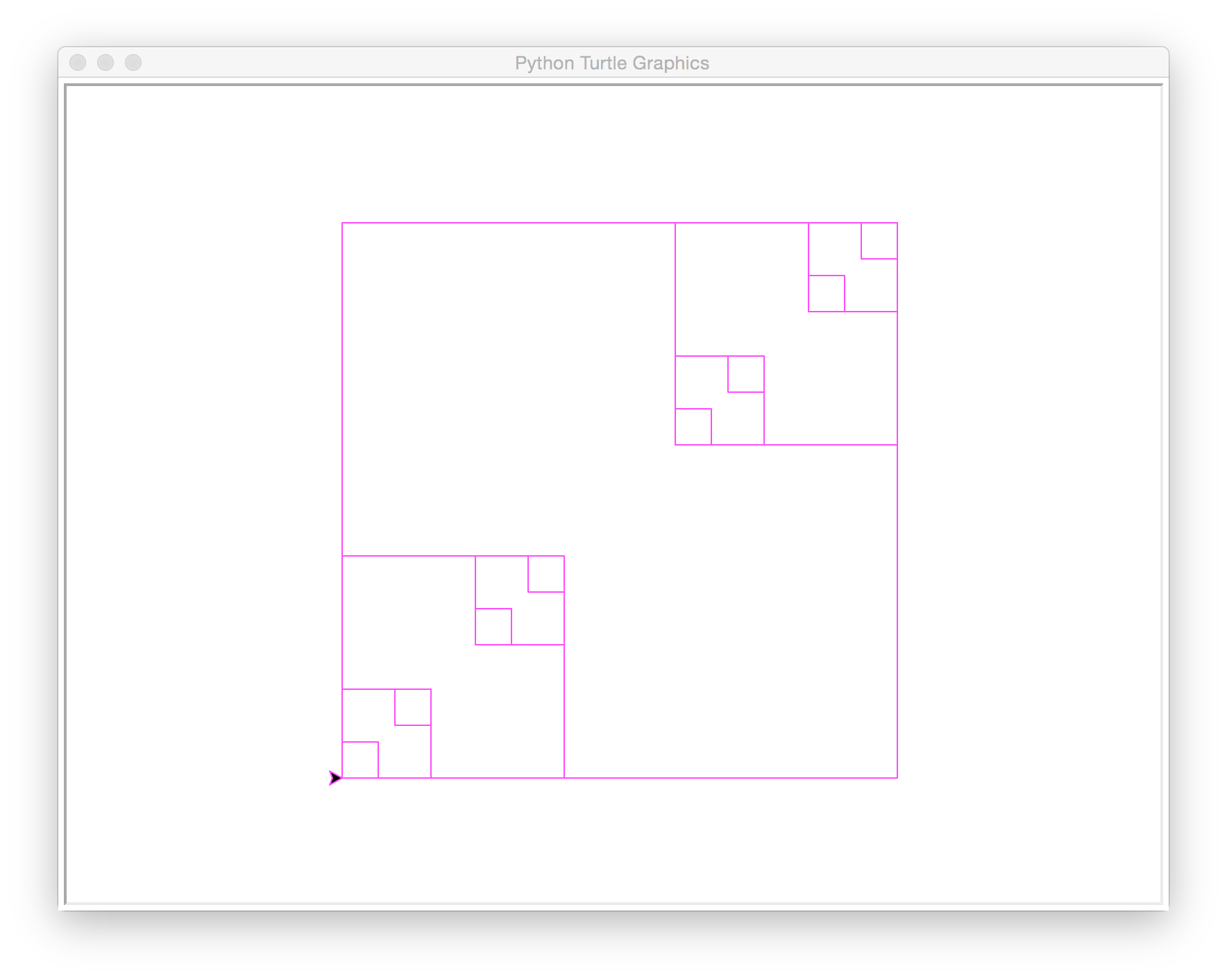
15 boxes drawn, 4723.2 total length

Example D.

windows(400, 0.75, 100, 'black')

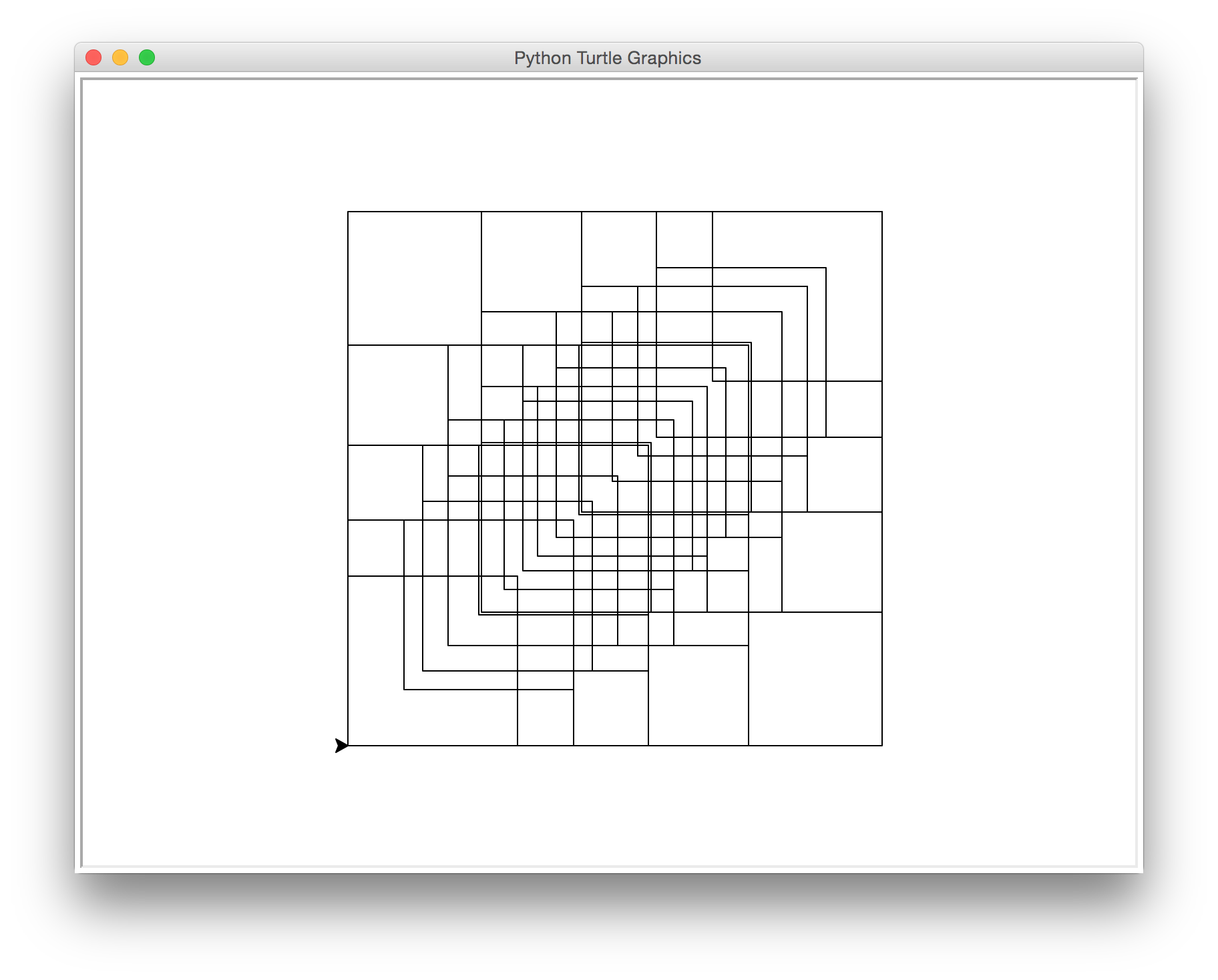
31 boxes drawn, 21100.0 total length

Task 3: Boxes (with clipped corners)

Write a fruitful recursive function called boxes that takes the following four parameters and produces squares in all four corners.

the length of the largest square
the shrink factor of the squares drawn at each of the four corners
the length of an edge of the smallest outer box
the color of the Turtle's pen

Once again, avoid approaching this design by trying to draw complete squares.

Instead, the fundamental pattern of the design can be broken down to a single side (repeated x4 via recursion to eventually make a square).

Here's a video demonstrating this approach:

boxes(400, 0.4, 100, 'red')

Example A.

boxes(400, 0.4, 100, 'magenta')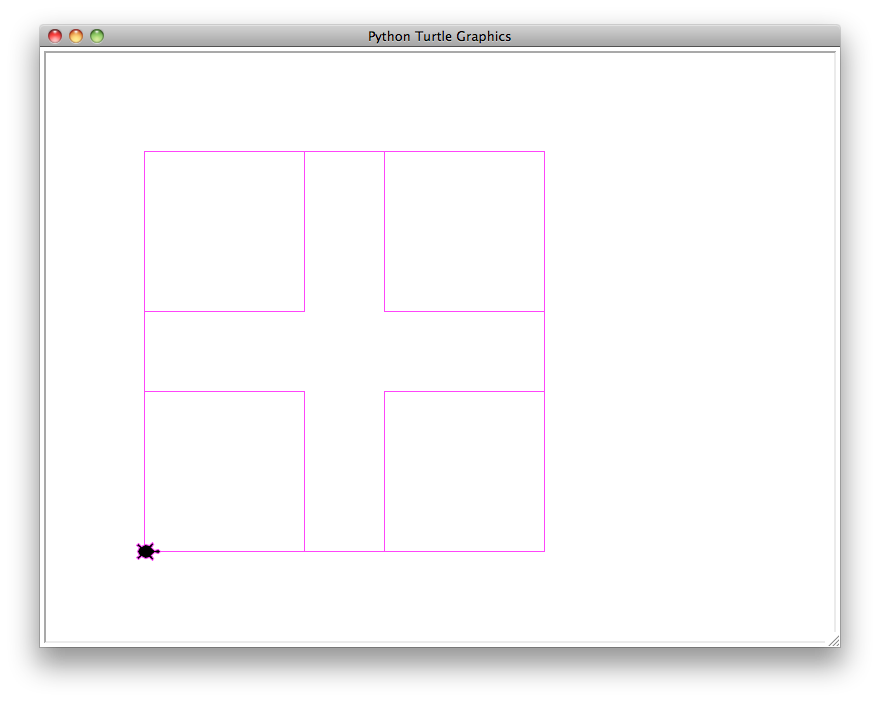

Observations

This example produces total of 5 boxes (1 outer box + 4 nested ones) and a total length of 4160.
- The largest box, has side length of 400.
- In each corner, there is a smaller box drawn with a side length of 160 (400 * 0.4 = 160).
There are no additional boxes drawn because the next set of corner boxes have a side length of 64 (160 * 0.4 = 64), which less than the smaller outer box length of 100.

Calculations

  2560 (4 smaller boxes with side length 160 x 4)
+ 1600 (1 outer box with side length 400 x 4)
==========
  4160

Example B.

boxes(400, 0.33, 30, 'magenta')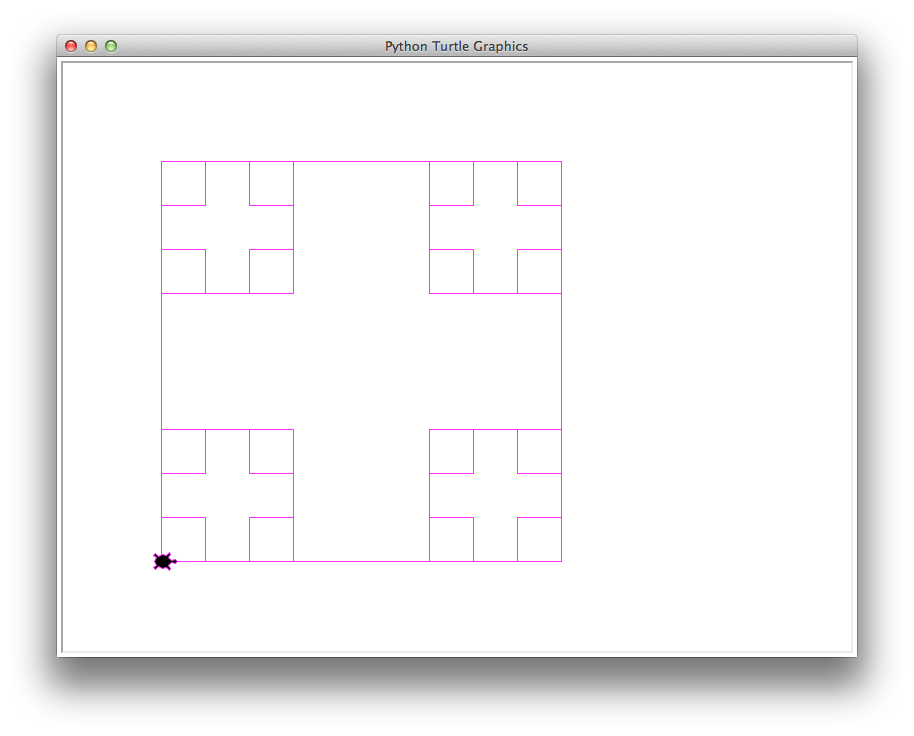

21 boxes, 6499.84 total length

Here's a diagram that shows the flow of how the recursive method boxes invokes itself (the first image is enlarged to show detail):

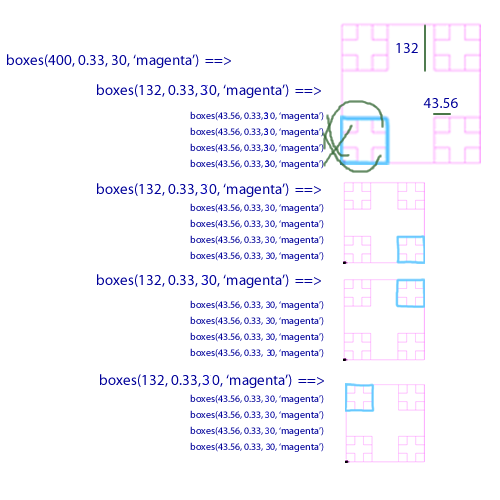
Example C.

boxes(400, 0.25, 15, 'magenta')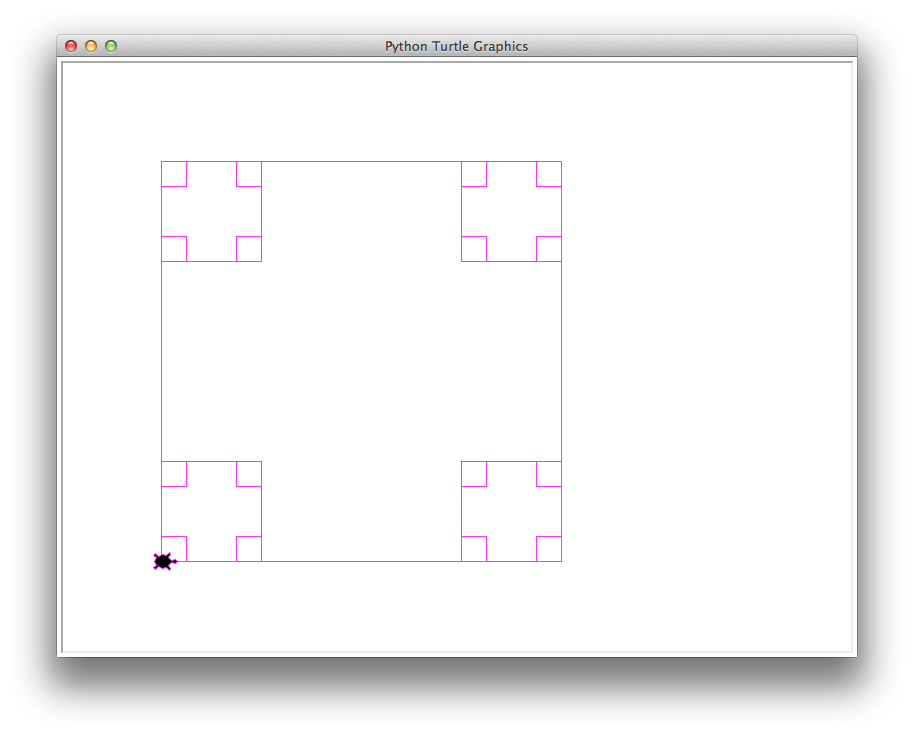

21 boxes, 4800 total length

Example D.

boxes(400, 0.4, 50, 'magenta')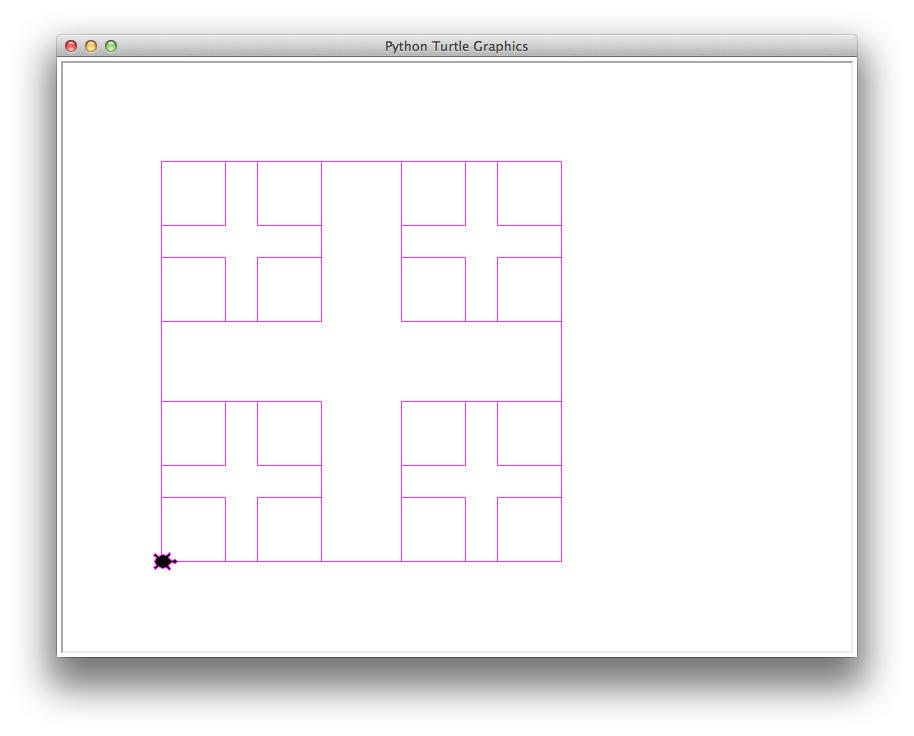

21 boxes, 8256 total length

Example E.

boxes(400, 0.44, 30, 'magenta')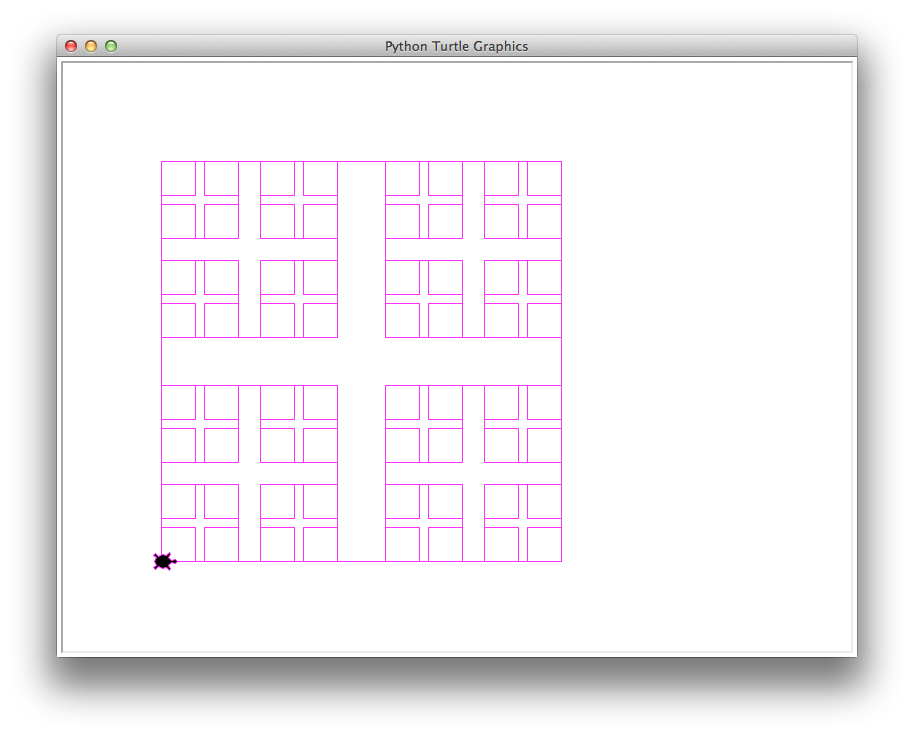

85 boxes, 18095.0016 total length

Example F.

boxes(400, 0.4, 10, 'magenta')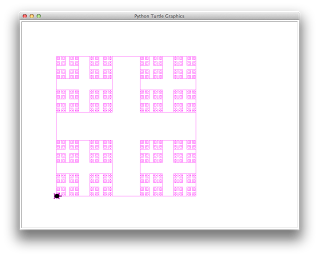

1365 boxes, 42072.576 total length