Graphic by Keith Ohlfs
CS111, Wellesley College, Spring 2000

Problem Set 4

Due: Friday, March 10 at 4:00 p.m.

[CS111 Home Page] [Syllabus] [Lecture Notes] [Assignments] [Programs] [Documentation] [Software Installation] [FAQ] [CS Dept.] [CWIS]

Reading

About this Problem Set

This problem set is intended to help you practice reading, writing, and understanding methods. You should think carefully about what patterns should be abstracted into methods and which patterns should be named as variables.

The purpose of this problem set is to give you experience with conditionals and recursion. Task 1 is a pencil-and-paper problem in which you will draw an execution diagram for a recursive buggle program. In Task 2, you will use conditionals to control a buggle to drop bagels at certain spots in a maze. In Task 3, you will use recursion in TurtleWorld to generate a self-similar picture. In Task 4, you will use recursion in BuggleWorld to produce quilt designs with bagels. The code for Tasks 2, 3, and 4 are available in the ps4_programs folder in the cs111 download directory on nike.

We have including working examples of the solutions to the programming problems in the Test folder that you download with the ps4_programs folder. It is a good idea to run these programs to get a feel for what we are asking you to do. Your solution should provide the exact same results as our solution (except as noted in the individual problem descriptions below).

Getting the problems to work is not enough to receive a perfect score on this assignment. You must also write your programs so that they are beautiful. Good programming style produces programs that are easy for others to read and understand. You should follow the style guidelines outlined in the reading as well as demonstrate that you understand the principle of when/how to use invariants.

With the introduction of conditionals and recursion, programming becomes much more challenging than on your first few assignments. It is a good idea to think carefully about how to solve your problems before you sit down at a computer and start writing code. It has been our experience that attempting to solve these sorts of problems while sitting at the computer is a recipe for disaster, because it can easily turn into a frustrating trial-and-error nightmare. Instead, we suggest that you form study groups and talk about solution strategies with your classmates before attempting to write any code. Once you have settled upon a strategy, we suggest that you write your Java code first using pencil and paper and simulate it in your head to check for its correctness. Only as a last step should you type in your code and test it on the computer.

Unlike previous problem sets, notes, hints, and suggestions for each homework problem are given on a separate page. We do want for you to have freedom to think about the problem in your own way. Reading the hints page is not required. It's main purpose is to help you think about the problem if you don't know how to get started.

How to turn in this Problem Set

Softcopy submission: Save your modified DeadEndWorld.java, SierpinksiWorld.java and BagelQuiltWorld.java files in the corresponding folders of the ps4_programs folder. Upload the entire folder (including all the other .java and .class files -- everything) to your ps4 drop folder.

Hardcopy submission: Turn in only one package of hardcopy materials. Please staple your files together with a cover page, and submit your hardcopy package by placing it in the box outside of Stanzi's office (E106, across from E101).

IMPORTANT NOTES:

  1. Pay careful attention to upper and lower case letters in the filenames.
  2. Once you have used Fetch to upload a file to the cs111 server, you should be sure to doublecheck that the file was actually uploaded. You can do this in Fetch by verifying that the file is now listed in your directory. Not only should you check that the file is listed, but you should check that it does not have a size of 0K. If the file isn't listed or if the size for the document is 0K, this means that there was an error in transferring it via Fetch and you must re-upload the document. When transferring a folder, you should check that its contents have been uploaded correctly. That is, you should be sure to check that every single file that you wish to submit has been uploaded correctly. Often times, although not always, you will see a message "Connection Failed" when there is an error in transferring your files.
  3. If you have trouble uploading files, it may be because you have reached the limits of your Nike file system quota. You will get an error message informing you that this is the problem. In this case, you need to delete some of your old files, either from your home directory or your drop folders (which are also counted toward your quota). To delete a file in Fetch, just drag it to the Trash.
  4. It is your responsibility to keep a personal back-up of every file that you submit electronically until you have received a grade for the assignment.

Task 1: Java Execution Model for a Recursive Method

The following recursive method is defined for the Recurser subclass of Buggle, which can be found in the file RecursionWorld.java within the Recursive Buggles folder of the lec10_programs folder:

	public void spiral (int n) {
		if (n > 0) {
			forward(n);
			left();
			spiral(n - 1);
			right();
			backward(n);
		}
	}

Consider the following run() method in the RecursionWorld subclass of BuggleWorld:

	public void run () {
		Recurser rita = new Recurser();
		rita.spiral(3);
	}

Draw a Java Execution Model diagram that shows all of the execution frames created by invoking the run() method on an instance of the the RecursionWorld class. Your diagram should depict the point in time when the invocation of run() returns. Although Java can discard an execution frame when control returns from it, you should not discard any frames when drawing your diagram.

In order to distinguish the state of rita at various points in time, you should show each variable as the row of a table whose columns are indexed by state names (such as s1, s2, s3, ...):
s1
s2
s3
...

Position
 

 
 

 
 

 
 

 

Heading
 

 
 

 
 

 
 

 

Color
 

 
 

 
 

 
 

 

BrushDown?
 

 
 

 
 

 
 

 

Each column represents the state of the buggle at some (perhaps several) points during the execution. The value of a variable in column si indicates the state of that variable when the buggle is in state si. If rita is in the same state at different points in time, you may reuse an existing state column rather than creating a new one. When evaluating an expression that refers to rita in the code portion of an execution frame, you should denote the value as the reference label R@si , where R (which should be circled) denotes rita and si denotes the state that rita was in when control evaluated the variable.

Please follow the usual conventions for drawing Java Execution Model diagrams. Strive to make your diagram as neat as possible.

Task 2: DeadEndWorld

In the DeadEndWorld problem, an eccentric buggle named Deanna loves to wander around in mazes finding all the dead ends. She loves it so much that she tries to get all her friends to find the dead ends in mazes, too. She does this by carrying around a bag of bagels as she explores mazes. Every time she finds a dead end, she leaves a bagel there so that her friends can be rewarded if they find the dead end, too. Deanna explores connected acyclic mazes. A connected acyclic maze is a maze in which there is a unique non-backtracking path from any point in the maze to any other. This means that it is always possible for Deanna to find all the dead ends in a particular maze! Here is an example of a connected acyclic maze:

It is possible to visit all the cells of a connected acyclic maze by using the "right-hand-on-the-wall" strategy. That is, if you always keep your right hand on a wall as you walk through such a maze, you will eventually visit all the cells and end up where you started. Along the way, you will visit some cells more than once (i.e., backtrack), but that's OK.

Your goal is to program members of the DeadEndBuggle class (such as Deanna) to drop bagels in all the dead ends of a particular maze by using the "right-hand-on-the-wall" strategy to visit cells in the maze until the buggle has explored the entire maze. Once the buggle has explored the entire maze and arrives at the start again, the buggle should not go through the maze again, but should just rest there. The buggle should leave a mark behind in every visited cell and a bagel in every dead end of the maze. Here is a snapshot of the above maze after Deanna is done exploring it:

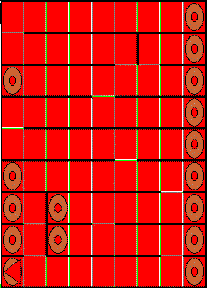
To begin this problem, use the Applet Viewer to run the DeadEndWorld.html applet within the Test subfolder of the ps4_programs folder that you downloaded for this assignment. This applet contains a working solution of the maze-navigating, bagel-dropping buggle. When you start this applet, you should see the maze shown in the first picture above. Every time you click on the Reset button, a new maze will be randomly generated. When you click Run, the buggle uses the right-hand-on-the-wall strategy to explore the maze and uses conditionals to figure out where to drop bagels.

Your goal is to develop a program that instructs the buggle to correctly explore entire mazes and drop bagels in all the dead ends. You will use Reset and Run to test your program on a variety of mazes.

You will implement your code in the file DeadEndWorld.java. This file contains two classes, as shown below:

public class DeadEndWorld extends MazeWorld {
   
  public void setup() {
   // setDimensions(11,19); // Change these numbers to get a different grid
  }
   
  public void run () {
    DeadEndBuggle deanna = new DeadEndBuggle();
    deanna.tick256();
  }
   
}

class DeadEndBuggle extends TickBuggle {
   
  // Override the default tick method of the TickBuggle class. 
  // Keep "right finger" of buggle on right wall to explore maze.
  // Drop bagels in dead ends.
  public void tick() {
    // Put your code here
  }
   
  // Returns true if this buggle should stop moving, and false otherwise.
  public boolean isDone () {
    // Replace this stub
    return false; 	
  }
   
   // Returns true if this buggle is a the position (1,1) and false otherwise.
  public boolean isAtStart() {
    // Replace this stub
    return false; 
  }
   
  // Add other auxiliary methods here.
}

The DeadEndWorld class is a subclass of the MazeWorld class, whose responsibility is to draw a connected acyclic maze. The run() method of the DeadEndWorld class creates Deanna and tells her to execute her tick() method 256 times. (As usual, a predetermined number of steps is icky; we will see how to get rid of this ickiness later in the course via recursion and iteration.) You do not need to modify the DeadEndWorld class in this problem.

In this problem, you should "teach" members of the DeadEndBuggle class how to follow the "right-hand-on-the-wall" strategy by filling in the details of the tick() method skeleton in that class. You should not use recursion to solve this problem! Rather, you should just use conditionals to control the state of the buggle, as discussed in the lectures on conditionals.

As part of your solution, you should define at least two auxiliary methods:

You may also define any other auxliary methods that you find helpful.

You should test your solution to make sure that it works properly on at least the first 3 mazes generated by the applet. The first three mazes include all the possible unique starting configurations. Your solution should behave exactly like the solution provided except that your buggle isn't required to "twitch" once she is finished with the maze and may end at the start in any orientation (heading).

Notes/Hints/Suggestions

Task 3: Sierpinski's Gasket

Sierpinski's gasket is a self-similar triangular entity discovered in 1916 by Polish mathematician Waclaw Sierpinski (1882-1969). In this problem we will investigate an approach for approximating Sierpinski's gasket.

Let sierpinski(levels, side) be the notation for a Sierpinski gasket with levels levels and side length side. Then a recursive mathematical definition of sierpinski is as follows:

The pictures below depict sierpinski(levels, side) for for levels = 1 through 5. These are approximations to the "true" self-similar Sierpinksi gasket, which is the limit of sierpinski(levels, side) as levels approaches infinity.

sierpinski(1,100)
sierpinski(2,100)
sierpinski(3,100)
sierpinski(4,100)
sierpinski(5,100)

In this problem you will define a Java method that uses a turtle to draw Sierpinski's gasket. To begin this problem, download the SierpinskiWorld folder from the ps5_programs folder in the CS111 download folder. The file SierpinskiWorld.java contains a subclass of Turtle named SierpinskiMaker with a stub for the following method:

public void sierpinski (int levels, double side);
Assume this turtle's pen is initially down. Draw a sierpinski gasket with levels levels whose outermost side length is side. The position, heading, and color of this turtle should be invariants of the method.

Flesh out the definition of the sierpinski method so that it draws the specified Sierpinski gasket and maintains the turtle's position, heading, and color as invariants. Your method should use recursion. You may define any auxiliary methods that you deem helpful.

SierpinskiWorld.java includes code that creates an instance of SierpinskiMaker and positions it toward the lower left hand corner of the screen facing east. A gasket whose lower left-hand corner is positioned at this starting point will be automatically centered in the TurtleWorld window.

Recall that the Turtle drawing primitives include the following:

public void fd (double n)
Move the turtle forward n steps. 

public void bd (double n); 
Move the turtle backward n steps.

public void lt (double angle);
Turn the turtle to the left angle degrees.  

public void rt (double angle);
Turn the turtle to the right angle degrees. 

public void pu (); 
Raise the turtle's pen up.

public void pd (); 
Lower the turtle's pen down.

Additionally, there are also versions of fd, bd, lt, and rt that take int parameters, so you can invoke these methods with either an integer or double floating-point value.

You should not need to use any other Turtle primitives other than those listed above. In fact, many solutions use only a subset of the primitives listed above.

Test your definition by specifying levels and side in the parameter window and then clicking on the Run button in the TurtleWorld window. The Reset button will clear the screen. Good parameter values are in the ranges [0 ... 8] for levels and [100 ... 400] for side. If your program hangs, you may need to "force quit" it by depressing the option, apple, and escape keys all at the same time.

The Test subfolder of the ps4_programs folder contains a working version of SierpinskiWorld.html that you can play with. Your solution should produce the same pictures as this test applet. It's worth noting that there are many possible ways to correctly decompose the problem, and the test applet uses only one possible approach. Thus, while you must produce the same designs as the test applet, you need not produce the designs in the same way as the test applet.

Notes/Hints/Suggestions

Task 4: Recursive Buggle Quilts

Quilt sales at the Buggle Bagel Rug Company have been flat recently. The market researchers at the company have determined that one factor accounting for the sluggish sales is the limited number of quilt sizes and quilt patterns offered by the company. In contrast, the recursively structured quilt patterns of their main competitor, the PictureWorld Quilt Company, have been selling like hotcakes.

To help improve sales, Quinton Buggle, the chief quilt designer at Buggle Bagel Rug, has developed a recursive bagel quilt pattern that can be used on a rug of any size. Here are examples of his pattern on square rugs with side lengths 16, 17, 18, and 19:

side = 16
side = 17

side = 18
side = 19

The fundamental repeated unit in these quilts is a triangle of bagels of size n, where n measures the number of bagels on a side. Here is such a triangle for n = 8:

Given a square rug with dimensions m x m, bagel triangles of size (m/2) are placed at the corners, and then the pattern is repeated in the smaller square bounded by the outer bagels in the center of the rug. Here (m/2) means integer division, as performed by Java. If m is odd, the result is truncated down to the nearest integer. For example, both 6/2 and 7/2 yield 3. Note that if m is even, all border cells of the square are covered with bagels, but if m is odd, the middle cell of each side of the square will not contain a bagel. Quinton has decided that the smallest square that should contain bagels is a 2x2 square. So the pattern is empty when applied to a 1x1 square.

In this problem, you are given a skeleton of the QuiltBuggle class and asked to define the following method in this class:

public void quilt(int side)
Assume that the buggle starts in the lower left-hand corner of a square whose side length is side, facing parallel to the bottom side. Drops bagels to form Quinton's pattern within this square, and returns to its initial position and heading.

Your quilt method should work for any integer; it should do nothing for side lengths <= 1. It should be defined using recursion. You will need to define numerous auxiliary methods, many of which themselves will be recursive.

You should write all your definitions within the QuiltBuggle class, which can be found in the file BagelQuiltWorld.java within the BagelQuilt folder of the ps4_programs folder. You can test your code by running the QuiltWorld.html applet. In addition to the usual BuggleWorld window, this applet displays a parameter window that allows you to change the side length of the BuggleWorld grid. Pressing the Reset button causes the grid to have the side length specified in the parameter window.

The Test subfolder of the ps4_programs folder contains a working version of BagelQuiltWorld.html that you can play with. Your solution should produce the same quilt designs as this test applet. It's worth noting that there are many possible ways to correctly decompose the problem, and the test applet uses only one possible approach. Thus, while you must produce the same designs as the test applet, you need not produce the designs in the same way as the test applet.

Notes/Hints/Suggestions