Graphic by Keith Ohlfs

CS111, Wellesley College, Spring 2000

Problem Set 3

Due: Monday, February 28 at 4:00 p.m.

[CS111 Home Page] [Syllabus] [Lecture Notes] [Assignments] [Programs] [Documentation] [Software Installation] [FAQ] [CS Dept.] [CWIS]

Reading

About this Problem Set

This problem set is intended to help you practice reading, writing, and understanding methods. You should think carefully about what patterns should be abstracted into methods and which patterns should be named as variables. Task 1 is a pencil-and-paper problem. The code for tasks 2 and 3 are available in the ps3_programs folder in the cs111 download directory on nike.

How to turn in this Problem Set

Save the modified KnitWorld.java and QuiltWorld.java files in the ps3_programs folder. Submit the entire ps3_programs folder to your drop folder on the cs111 server. Turn in a hardcopy of the invocation tree from task 1 and your modified KnitWorld.java and QuiltWorld.java.

When submitting your hardcopies, we ask that you turn in only one package of materials. Please staple your files together with a cover page, and submit your hardcopy package by placing it in the box outside of Stanzi's office (E106, across from E101).

IMPORTANT NOTES:

  1. Exam 1 will be held in class on Thursday, March 2. It will cover material in lecture through Thursday, February 17, Problem Sets 1 through 3, and Labs 1-4. Even though Problem Set 3 may not be graded by the time of the exam, solutions for Problem Set 3 will be made available soon after the due date so that you may study them for the exam.
  2. Pay careful attention to upper and lower case letters in the filenames.
  3. Once you have used Fetch to upload a file to the cs111 server, you should be sure to doublecheck that the file was actually uploaded. You can do this in Fetch by verifying that the file is now listed in your directory. Not only should you check that the file is listed, but you should check that it does not have a size of 0K. If the file isn't listed or if the size for the document is 0K, this means that there was an error in transferring it via Fetch and you must re-upload the document. When transferring a folder, you should check that its contents have been uploaded correctly. That is, you should be sure to check that every single file that you wish to submit has been uploaded correctly. Often times, although not always, you will see a message "Connection Failed" when there is an error in transferring your files.
  4. If you have trouble uploading files, it may be because you have reached the limits of your Nike file system quota. You will get an error message informing you that this is the problem. In this case, you need to delete some of your old files, either from your home directory or your drop folders (which are also counted toward your quota). To delete a file in Fetch, just drag it to the Trash.
  5. It is your responsibility to keep a personal back-up of every file that you submit electronically until you have received a grade for the assignment.

Task 1: Invocation Tree for smallDesign()

As discussed in class, an invocation tree is an abbreviated version of a Java Execution Model. It contains a node for each method called during the execution of a program. Each node contains the receiver of the method invocation, the name of the method, the values of its parameters, and (where applicable) its result. There is an edge connecting each "parent" node to the "children" nodes for the method invocations encountered directly within the body of the parent. The children nodes are all shown at the same vertical level, arranged from left to right in the order of their execution.

For example, consider invocation tree for fourSame(greenWedge) that was derived in class:

	public Picture fourSame (Picture p) {
		return fourPics(p, p, p, p);
	}

	public Picture fourPics (Picture p1, Picture p2, Picture p3, Picture p4) {
		return above(beside(p1,p2), beside(p3,p4));
	}

Below is an invocation tree for the invocation SPW.fourSame(P1), where SPW symbolizes the SimplePictureWorld object that receives the method invocation and P1 denotes the greenWedge Picture object. Each node contains the value of the receiver, followed by the method name, followed by the actual parameters enclosed in parentheses. The result of invoking the method is then shown after a colon. Note that the nodes at the same level are drawn from left to right in the order that the methods are invoked.

EXECUTION LAND

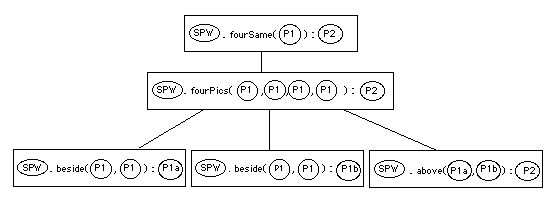
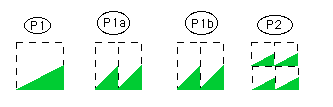
The Objects referenced in the invocation tree are shown below:

OBJECT LAND

In this problem, you will draw an invocation tree for the invocation of a method that computes a smaller version of the design() method introduced in lecture. This method, called "smallDesign()", is defined as follows: 

 
	public Picture smallDesign (Picture p) {
		return rotations2(rotations2(p));
	}
	
	public Picture rotations2 (Picture p) {
		return fourPics(p, clockwise90(p), clockwise180(p), clockwise270(p));
	}	
	
	public Picture fourPics (Picture p1, Picture p2, Picture p3, Picture p4) {
		return above(beside(p1,p2), beside(p3,p4));
	}

For this problem, you are to draw a complete invocation tree for the invocation smallDesign(P1), where P1 represents the green wedge shown in the example above. To represent each Picture object, you should sketch the picture represented by that object below your invocation tree. Show the unit square in a dotted line around the picture object, as shown above. Give your sketch of the picture a label, such as P1, P2, P1a, etc., and use that label to reference the object in the invocation tree, as shown in the diagram above. You should label the part of your drawing that contains the invocation tree "EXECUTION LAND", and the part of the drawing that shows the Picture objects "OBJECT LAND" as in the example above. In your invocation tree, all children of the same parent should appear at the same vertical level. (You may need to turn your paper sideways, and perhaps tape two pieces of paper together to fit all the nodes).

Task 2: Knit Picking

Escher's Knitting Patterns

Dutch artist M. C. Escher is renowned for creating artwork based on interlocking patterns and visual playfulness. Here we will experiment with "knitting patterns" that Escher himself experimented with in 1943. (For more details on Escher's artwork, see M.C. Escher: Visions of Symmetry by Doris Schattschneider, W.H. Freeman and Company, 1990).

Escher's knitting patterns were based on the following two primitive patterns that he designed:


Pattern A
Pattern B

We will call these patterns A and B. We can make many variants of A an B by rotating them, flipping them, and painting their stripes different colors. These variants of A and B can be combined to form an amazing number of patterns that resemble the weave patterns of knitted yarn. For example, study the following four knitting patterns, all of whose basic squares are versions of A and B that have been rotated, flipped, and colored in various ways.

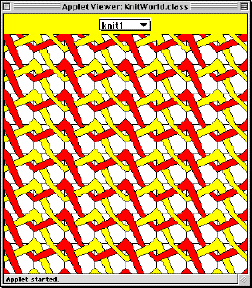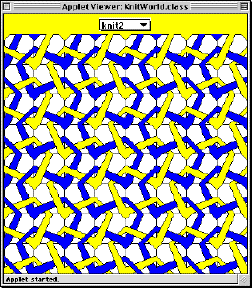Playing with Knitting Patterns in PictureWorld

PictureWorld is a perfect tool for experimenting with Escher's knitting patterns. The file KnitWorld.java within the ps3_programs folder contains several methods that aid in this experimentation. Colored versions of the A and B patterns are created by the following two black-box methods in KnitWorld.

	public Picture A(Color c1, Color c2, Color c3, Color c4, Color c5);
	public Picture B(Color c1, Color c2, Color c3, Color c4, Color c5);

The five color arguments of A and B paint the patterns in the way indicated by the following examples:


A(Color.red, Color.blue,
Color.green, Color.yellow, Color.magenta);
B(Color.red, Color.blue,
Color.green, Color.yellow, Color.magenta);

The tileKnit method is useful for constructing many simple knitting patterns:

 	public Picture tileKnit (Picture p1, Picture p2, Picture p3, Picture p4) {
 		return fourSame(fourSame(fourPics(p1, p2, p3, p4)));
 	}

The fourSame and fourPics methods are the same as those presented in lecture:

 
 	public Picture fourSame (Picture p) {
 		return fourPics(p, p, p, p);
 	}
 	
 	public Picture fourPics (Picture p1, Picture p2, Picture p3, Picture p4) {
 		return above(beside(p1,p2), beside(p3,p4));
 	}
 

Using the above methods, plus the usual picture combinators of PictureWorld, it is possible to make pictures for all four knitting patterns shown above. Here is a knit1() method, parameterized over two colors, that generates the knit1 pattern shown above:

 
	public Picture knit1(Color c1, Color c2) {
		Picture A1 = A(c1, c2, c1, c1, c2);
		Picture B1 = B(c2, c1, c2 ,c2, c1);
		return tileKnit(A1,B1,A1,B1);
	}
 

The knit2() method is similiar in structure to knit1(), but uses different colorings, flips, and rotations:

	public Picture knit2(Color c1, Color c2) {
		Picture A1 = A(c1, c2, c1, c2, c1);
		Picture B1 = B(c2, c1, c2 ,c1, c2);
		return tileKnit(flipHorizontally(B1),
 		               flipHorizontally(A1),
 		               clockwise180(B1),
 		               clockwise180(A1));
	}
 

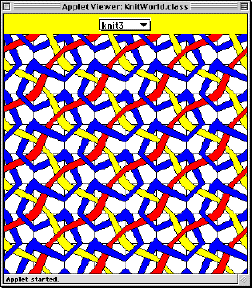
The knit3() method is parameterized over three colors rather than four: 

	public Picture knit3(Color c1, Color c2, Color c3) {
		return tileKnit(B(c1,c2,c1,c3,c1),
 		               clockwise90(B(c1,c3,c2,c2,c1)),
 		               flipVertically(B(c1,c3,c1,c2,c1)),
 		               flipVertically(clockwise90(A(c1,c2,c3,c3,c1))));
	}

 

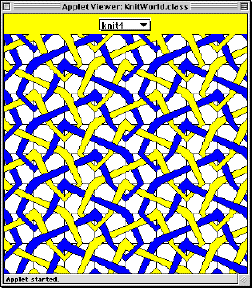
The knit4 pattern has a more complex repetition pattern than can be described by tileKnit(). The following knit4() method captures this pattern: 

	public Picture knit4(Color c1, Color c2) {
		Picture tile1 = fourPics(B(c1,c2,c1,c2,c1),
 		                        clockwise270(A(c1,c2,c1,c1,c2)),
 		                        flipVertically(B(c1,c2,c1,c2,c1)),
 		                        clockwise90(flipVertically(B(c2,c1,c2,c2,c1))));
		Picture tile2 = fourPics(A(c2,c1,c2,c1,c2),
 		                        clockwise270(B(c2,c1,c2,c2,c1)),
 		                        flipVertically(A(c2,c1,c2,c1,c2)),
 		                        clockwise90(flipVertically(A(c1,c2,c1,c1,c2))));
		return fourSame(fourPics(tile1, tile2, tile1, tile2));
	}

 

Your Knitting Pattern Problems

In this problem, you will define methods that draw the following two knitting patterns:

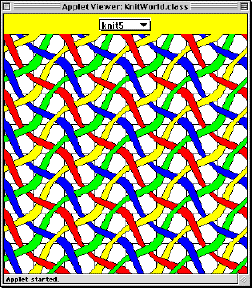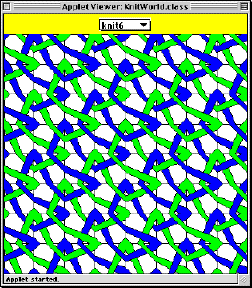The file KnitWorld.java contains the skeletons of two methods that you should flesh out :

	
	public Picture knit5(Color c1, Color c2, Color c3, Color c4) {
       // Put your definition here.
	}
 	
	public Picture knit6(Color c1, Color c2) {
       // Put your definition here.
	}

knit5() is parameterized over four colors, while knit6() is parameterized over two colors. The particular knit5 pattern shown above is created by the invocation knit5(Color.red, Color.yellow, Color.blue, Color.green). The particular knit6 pattern shown above is created by the invocation knit6(Color.green, Color.blue).

To begin this problem, first study the knit1() through knit4() methods above and convince yourself that they do in fact draw the four knitting patterns shown in the previous section. Your solutions to knit5() and knit6() will be similar to the knit1() through knit4(). Next, you should carefully study the knit5 and knit6 patterns to determine which rotations, flips, and colorings of the basic patterns A and B are employed. The final step is to encode your findings in Java code in the method bodies of knit5() and knit6(). You may find it helpful to define your own auxiliary methods in addition to defining knit5() and knit6().

Note that you may view all the patterns above in AppletViewer by loading the KnitWorld.html file found in the Test folder within the ps3_programs folder.

Task 3: QuiltWorld

Bertha Buggle, co-founder of the Buggle Bagel Ruggle Company, has been looking for new ways to expand her company's product line. Although the bagel rugs marketed by the company are popular, they are difficult to manufacture because of the labor costs (each rug is hand-drawn by a Buggle) and and raw material costs (bagels cost more than you think!). Bertha thinks the company should diversify to produce other products with interesting designs, such as quilts,wallpaper, and sweaters. Bertha is currently experimenting with the picture drawing software presented in CS111 to design quilts. Here is an example of one of Bertha's quilt designs, which we will call quilt.

You and several other CS111 students have been hired as interns at the Buggle Bagel Ruggle Company to help Bertha design quilts. Your project is to use PictureWorld to generate the quilt design shown above. There is a file called QuiltWorld.java in the ps3_programs folder. All the methods that you will define for this problem will be in the QuiltWorld class. Your goal is to flesh out the skeleton of the quilt() method so that it returns a picture corresponding to the quilt shown above. This picture is ultimately generated by combining primitive pictures generated by the following two black-box methods:
public Picture patch (Color c)
Returns a rectangular patch of color c with a black border that fills a given picture frame.

public Picture triangles(Color c1, Color c2)
Returns a picture that consists of two triangles filling the given picture frame: a black-bordered triangle of color c1 in the lower left corner of the frame; and a black-bordered triangle of color c2 in the upper right corner of the frame.

For example, below are the pictures generated by some sample invocations of these methods:

patch(Color.red);
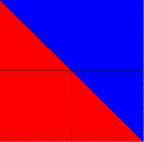
triangles(Color.red, Color.blue);

Divide, Conquer, and Glue

The key to solving the problem of defining quilt() is to note that the picture can be decomposed into smaller pictures that are used more than once in the larger picture. For example, the upper right quadrant is a picture that we'll call corner: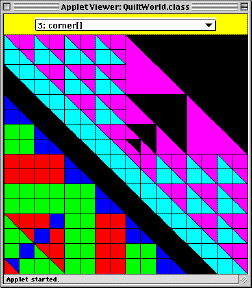

The whole picture can be decomposed into four copies of corner that have different rotations. Once we figure out how to define the corner picture, we can combine four rotated copies of the picture to form the desired quilt picture. This is an excellent illustration of the divide, conquer, and glue problem solving strategy we will use throughout this course:

  1. Divide the problem into subproblems. Here there is one subproblem: defining corner.
  2. Conquer the subproblems by solving them. In this case, the solution to the subproblem is a picture named corner.
  3. Glue the solutions to the subproblems together to form the solution to the whole problem. Here, we combine four rotated versions of corner to construct quilt.
But how do we solve the problem of defining the corner picture? By applying the divide, conquer, and glue strategy again! In this case, corner naturally decomposes into four quadrants: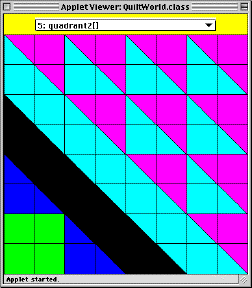

quadrant2
quadrant3

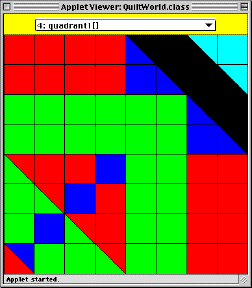quadrant1
quadrant2

We give the names quadrant1, quadrant2, and quadrant3 to each distinct pattern. We notice that quadrant2 is used twice in the corner! We can continue to use divide, conquer, and glue to decompose each quadrant above into smaller and smaller pictures. When does the process stop? When we get to pictures so small that they are trivial to solve! In this case the trivial pictures are those generated by the patch() and triangles() methods.

Auxiliary Methods

A general principle of computer science is "never write any piece of code more than once". If you find yourself writing the same or similar code more than once in your program, you should instead write methods that capture the patterns of the repeated code and invoke the methods instead.

The divide, conquer, and glue process of defining quilt() naturally exposes the need for numerous auxiliary methods. As part of working on this assignment, you should define and use the following methods. Skeletons for all of these methods can be found in QuiltWorld.java.

public Picture patch_2x2 (Color c)
Returns a picture consisting of four rectangular patches of color c with black lines between the patches. (Remember that patch(c) returns a picture with a black border.)

public Picture triangles_2x2 (Color c1, Color c2)
Returns a picture similar to triangles(c1, c2) except that each large triangle is composed out of four smaller fragments (two triangles and two rectangles).

public Picture LL (Picture p)
Returns a picture which divides the picture space into four quadrants and places the given picture in the lower left corner.

public Picture LLNest (Picture p1, Picture p2)
Returns a picture which places picture p2 over the lower left corner of picture p1.

Here are example invocations of the four methods above:

patch_2x2(Color.red);
triangles_2x2(Color.red, Color.blue);

LL(triangles(Color.red, Color.blue));
LLNest(patch(Color.red), triangles(Color.red, Color.blue));

Completing the Assignment

All of the methods in the PictureWorld and QuiltWorld contracts are available to you. At a minimum, you should have methods that correspond to each pattern described above. The QuiltWorld.java file has skeletons for all the methods that you must define. In addition to that, you should define additional methods which capture patterns that are used over and over again. It is also helpful to define local variables within your methods to give names to pictures that you generate as part of your solution.

Hints