CS111 Lecture: Lists, Memory Diagrams, Mutable vs. Immutable Values¶
Table of Contents:
- Review: You can use [] to make lists in python
- Review: Indexing
- Model: List Memory Diagrams
- Diagrams and Indexing with Nested Lists
- Some other ways to make lists (some you've seen before)
- You can mix and match different types within a list (heterogeneous lists)
- Lists are sequences
- Lists are mutable
- Pop Quiz
- Tuples
- Tuple Assignment
- Optional: Enumerations
1. Review: You can use [ ] to make lists in python¶
A Python list is a sequence of values, which are called elements of the list. A list can be created by writing a sequence of comma-separated expressions delimited by square brackets.
Lists themselves are Python objects, and so can be named by variables.
Below are some homogenous lists, which means that all elements of the list have the same type.
primes = [2, 3, 5, 7, 11, 13, 17, 19]
states = ['Alabama', 'Michigan', 'California', 'Wyoming']
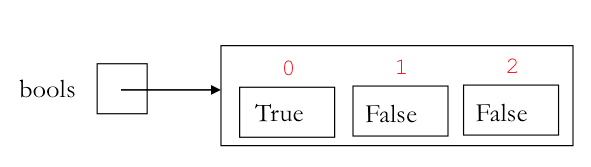
somebools = [1<2, 1==2, 1>2]
somenums = [3+4, 5*6, 7-9, 50/5]
somestrings = ['ab' + 'cd', 'ma'*4]
anEmptyList = [] # A string with zero elements
Note: If an element is an expression, such as 1<2 or 3+4, it's first evaluated to a value, and then stored in the list.
So, can you guess what is stored in somebools, somenums, and somestrings?
somebools
somenums
somestrings
type(primes)
type(states)
2. Review: Indexing lists¶
To access individual elements of the list as opposed to the entire list, we use indices.
Very Important Note: The nonnegative indices always start at 0 and end at a number one less than the length of the list.
primes = [2, 3, 5, 7, 11, 13, 17, 19]
Accessing the first element of the list, using index 0:
primes[0]
# how do you access 11 in the list?
# Your code here
primes[4]
What happens if you write primes[8]? Can you explain it?
primes[8]
Now that we reviewed how lists are created and indexed via Python code, let's discuss a model of how lists are stored in the computer memory.
3. Model: List Memory Diagrams¶
We draw lists with n elements as a big box containing n smaller boxes (slots) that hold the n elements. Each smaller box or slot is written with an index number above the box. Organizing lists with these diagrams help us understand ways to interact with lists.
Below are two examples of memory diagrams for two different lists. Each list is assigned to a variable. To depict a variable using memory diagrams we simply write the name of the variable and a box to the right. When the value of the variable is a list, we draw an arrow from the variable box to the big box representing the list.
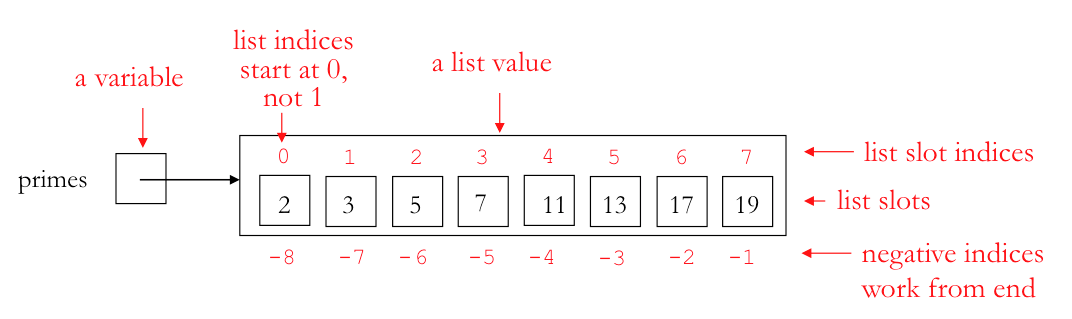
For a length-n list, slots can also be addressed by indices that go (right to left) from -1 to -n.
primes[-2]
# give two different ways to access the number 13 (using positive and negative indices)
# Your code here
primes[5]
primes[-3]
4. Diagrams and Indexing with Nested Lists¶
Often, we will work with lists of lists (or nested lists). We can create and index them similarly to simple lists
# Let's create some nested lists
animalLists = [['fox', 'raccoon'], ['duck', 'raven', 'gosling'], [], ['turkey']]
lottaNumbers = [[18, 19, 20], [5, 34, 2], [3], [10, 20], [37, 54]]
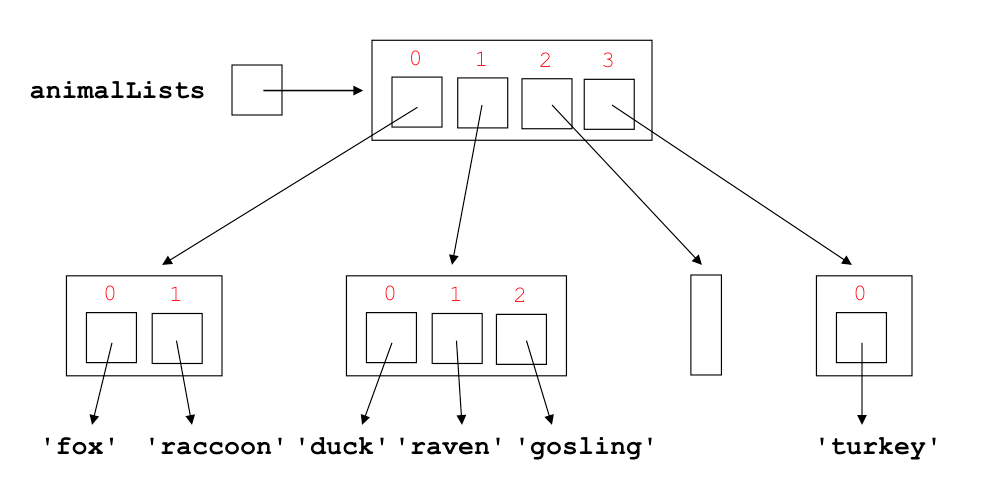
We can assign list elements to new variables:
mammals = animalLists[0]
mammals
mammals[1]
animalLists[0][1]
We just showed two different ways to refer to the same value, "raccoon".
animalLists[1][0]
# What indices return "turkey" in animalLists[???][???]
# Your code here
animalLists[3][0]
# What indices return "gosling" in animalLists[???][???]
# Your code here
animalLists[1][2]
5. Some other ways to make lists (some you've seen before)¶
# Using list on a range()
oddies = list(range(1,10,2))
# Using split() on a string
lyrics = 'call me on my cell'.split()
# Using list on a string
letters = list("happy")
# By concatenation other lists
ints = [7, 2, 4] + [8, 5] + [1, 0, 9, 3]
# By repeating a list
reps = [7, 2, 4] * 3
print(oddies)
print(lyrics)
print(letters)
print(ints)
print(reps)
6. You can mix and match different types within a list (heterogeneous lists)¶
Here's a heterogeneous list, containing several different types of elements.
stuff = [17, True, 'Wendy', None, [42, False, 'computer']]
For you: Try to predict the value for each of the following expressions:
stuff[0] + stuff[4][0]
stuff[2] + stuff[4][2]
stuff[0] + stuff[4][2]
7. Lists are sequences¶
len: Length of a list¶
We will use the familiar built-in function len() to find the length of a list.
len(primes)
# Can you guess what the length of this nested list will be?
animalLists = [['fox', 'raccoon'], ['duck', 'raven', 'gosling'], [], ['turkey']]
# Check your guess
len(animalLists)
What about:
len(animalLists[1])
len(lottaNumbers)
len(stuff)
len([])
List slicing¶
Use the slicing operator : to create a new list that contains some of the elements of the original list.
primes
primes[2:6]
primes[2:]
primes[1:7:2]
# First slice index defaults to 0 when step is positive
primes[:5:2]
# Second slice index defaults to length of list when step is positive
primes[3::2]
# Can have negative step
primes[7:1:-2]
primes[-1:-8:-1]
# What are default first and second indices when step is negative?
primes[::-1]
Other sequence operations¶
13 in primes
15 in primes
15 not in primes
min([6,2,3,9,5,8])
max([6,2,3,9,5,8])
max(['one', 'two', 'three','four', 'five'])
# Lists are compared in dictionary order, where each element is treated like a "character"
[5,3] < [6, 2, 4]
[5,3] < [5, 2, 4]
# Explain this result:
max(animalLists)
8. Lists are mutable¶
In this case mutation means:
- we can change the contents of the list slots
- we can change the structure of the list by adding and removing list slots. We will see three list methods for doing this:
append,pop, andinsert.
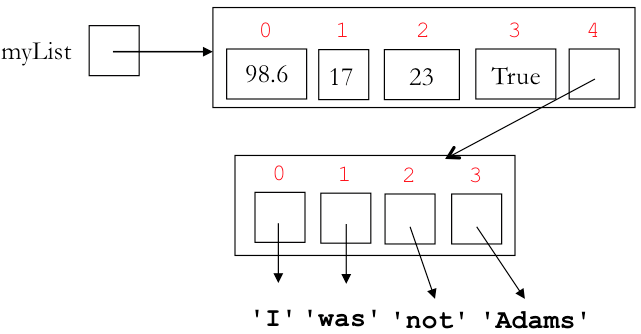
Let's start with myList¶
myList = [17, 3.141, True, None, ['I', 'am', 'Sam']]
myList
We can change the contents of list slots via the assignment operator =¶
myList[1] = myList[0] + 6
myList[3] = myList[0] > myList[1]
myList[4][1] = 'was'
myList # to see contents of myList
We change the list structure by appending a new item to the end¶
myList.append(42)
myList[4].append('Adams')
myList # to see what is in there
pop examples¶
A method to remove items from a list.
Let's see first what's in the list myList, which was already mutated in the previous cells in this Notebook:
myList
myList.pop(1)
Notice that pop returns the value that it removed from the list.
myList
myList[3].pop(2)
myList
myList.pop()
Notice that when we don't use an argument for pop, by default it removes the very last element.
myList
insert examples¶
insert is a method that takes two parameters:
- the index of the list slot where the insertion will hapen;
- the value to be inserted
myList.insert(0, 98.6)
myList
myList[4].insert(2, 'not')
myList
Aliasing¶
Aliasing creates another variable name for the same object in Python. We can depict these with memory diagrams by simply drawing another box for the variable with the variable name on the left. The contents of the variable box will have an arrow pointing to that object.
Aliasing Example 1¶
Use memory diagrams to explain the the list structures that result from executing the following statements in order
L1 = [7, 4]
L2 = [7, 4]
L3 = L2
L2[1] = 8
L4 = [L1, L1, L2, L3]
L4[2].append(5)
The final list diagram is the one below. A key feature of this diagram is aliasing, which means that the same list objects can be accessed by different expressions involving variables and lists. For example, the expressions L1, L4[0], and L4[1] all refer to the same 2-element list object [7,4], while the expressions L2, L3, L4[2], and L4[3] all refer to the same 3-element list object [7,8,5]. Memory diagrams involving lists are essential for understanding aliasing, which is essential for understanding how operations that mutate lists will behave.
![This picture depicts a memory diagram for the aliasing example involving L1, L2, L3, L4, and L4. In the final diagram L1 is a list of the two elements 7 and 4, and L2 and L3 are aliases for the same three-element list with elements 7, 8, and 5. L4 is a four-element list: L4[0] and L4[1] are aliases for L1, and L4[2] and L4[3] are aliases for L2.](aliases1ListDiagram.png)
== tests for structural equality, but not aliasing¶
When used to compare two lists, Python's equality operator == returns True if and only if (1) the two list have the same length and (2) all the corresponding indices have values for which == returns True. This is called structural equality of lists.
As shown below, two lists can be structurally equal via == even if they are not aliases of the same lists. So == is too weak a test for determining aliases:
L1b = [7, 4]
L2b = [7, 4]
L3b = L2b
print('L1b==L2b', L1b==L2b)
print('L1b==L3b', L1b==L3b)
print('L2b==L3b', L2b==L3b)
Python's built-in id function¶
Python's id() function returns a long number that is a unique identifier for each object in a memory diagram. You can think of it as being the abstract address of the object in memory. If two list expressions have the same id, they must be represented by a single list box in a memory diagram (i.e., they are aliases for the same list value). If two list expressions have different ids, they must be represented by two different list boxes in a memory diagram.
For example, id can tell us that L2b and L3b are aliases for the same list, but that L1b is a different list:
print('id(L1b) =>', id(L1b))
print('id(L2b) =>', id(L2b))
print('id(L3b) =>', id(L3b))
In our bigger running example, because L1, L4[0], and L4[1] are aliases of the same list, all return the same number using the id function:
print('id(L1) =>', id(L1))
print('id(L4[0]) =>', id(L4[0]))
print('id(L4[1]) =>', id(L4[1]))
Because L2, L3, L4[2], and L4[2] are aliases of a list that is different than L1, all share an id that is different that the id for L1:
print('id(L2) =>', id(L2))
print('id(L3) =>', id(L3))
print('id(L4[2]) =>', id(L4[2]))
print('id(L4[3]) =>', id(L4[3]))
For this reason, id is handy for reasoning about aliasing/sharing in memory diagrams.
Python's is operator¶
Python's binary is operator returns True if its two operands have the same id; otherwise it returns False. It is also very useful for reasoning about aliasing/sharing in memory diagrams.
In the small example, is shows that L2b and L3b are the same list, but they are different from L1b:
print('L1b is L2b =>', L1b is L2b)
print('L1b is L3b =>', L1b is L3b)
print('L2b is L3b =>', L2b is L3b)
In the larger running example, it shows which expressions are aliases for the same lists:
print('L1 is L2 =>', L1 is L2)
print('L2 is L3 =>', L2 is L3)
print('L1 is L4[0] =>', L1 is L4[0])
print('L1 is L4[1] =>', L1 is L4[1])
print('L1 is L4[2] =>', L1 is L4[2])
print('L2 is L4[1] =>', L2 is L4[1])
print('L2 is L4[2] =>', L2 is L4[2])
print('L2 is L4[3] =>', L2 is L4[3])
print('L4[0] is L4[1] =>', L4[0] is L4[1])
print('L4[1] is L4[2] =>', L4[1] is L4[2])
print('L4[2] is L4[3] =>', L4[2] is L4[3])
Aliasing Example 2¶
As a second example of aliasing, consider modifications to the memory diagram at the end of the insert examples:
We begin by introducting the alias list2 for myList:
list2 = myList
id(list2)
id(myList)
list2 is myList
We also inroduce adamsList as an alias for list2[4]
adamsList = list2[4]
adamsList
adamsList is list2[4]
Without a memory diagram, it's bit less obivous that adamsList is also an alias for myList[4]:
adamsList is myList[4]
Now let's make myList[1] be an alias for myList[4]:
myList[1] = myList[4]
Finally, let's change adamsList[2] to be 'JQ':
adamsList[2] = 'JQ'
Can you predict the printed represenation of list2 now? Without memory diagrams, this can be very challenging to predict!
list2
It turns out that the list adamsList has four other aliases in this example:
print('myList[1] is adamsList =>', myList[1] is adamsList)
print('myList[4] is adamsList =>', myList[4] is adamsList)
print('list2[1] is adamsList =>', list2[1] is adamsList)
print('list2[4] is adamsList =>', list2[4] is adamsList)
This can be very challenging to understand without the aid of the final memory diagram for this example:
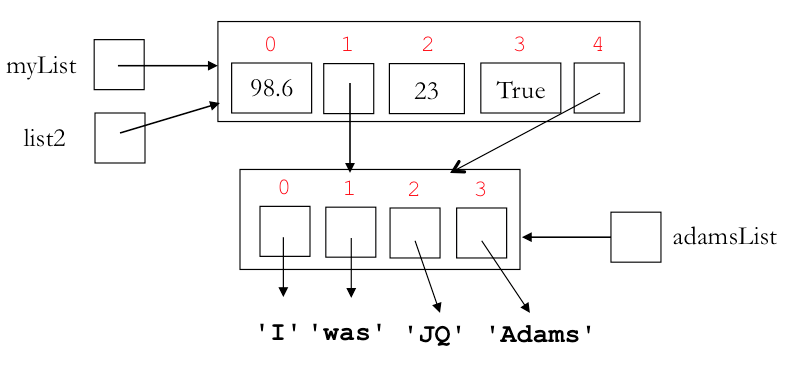
9. Pop Quiz¶
What is the value of c[0] at the end of executing the following statements? Draw a memory diagram to justify your answer!
a = [15, 20]
b = [15, 20]
c = [10, a, b]
b[1] = 2*a[0]
c[1][0] = c[0]
c[0] = a[0] + c[1][1] + b[0] + c[2][1]
# Only check this after you've made a prediction!
c[0]
Let's break down some of the code to see what is going on. Although a and b seem to have the same value, they occupy different addresses in the memory, so, they are not the same object.
a = [15, 20]
b = [15, 20]
print('id(a) =>', id(a))
print('id(b) =>', id(b))
print('a is b =>', a is b)
In the list c, c[1] is an alias for a and c[2] is an alias for b, but they are not aliases for each other:
c = [10, a, b]
print('c[1] is a =>', c[1] is a)
print('c[2] is b =>', c[2] is b)
print('c[1] is c[2] =>', c[1] is c[2])
Because of aliasing, changing a slot in b changes the same slot in c[2], but not in a or c[1]:
b[1] = 2*a[0]
print('b =>', b)
print('c[2] =>', c[2])
print('a =>', a)
print('c[1] =>', c[1])
Because c[1] is an alias for a, changing c[1][0] changes a[0] but does not affect b or c[2]:
c[1][0] = c[0]
print('a =>', a)
print('c[1] =>', c[1])
print('b =>', b)
print('c[2] =>', c[2])
Now we can determine the summands of a[0] + c[1][1] + b[0] + c[2][1]
print('a[0] =>', a[0])
print('c[1][1] =>', c[1][1])
print('b[0] =>', b[0])
print('c[2][1] =>', c[2][1])
print('a[0] + c[1][1] + b[0] + c[2][1] =>', a[0] + c[1][1] + b[0] + c[2][1])
c[0] = a[0] + c[1][1] + b[0] + c[2][1]
print('c[0] =>', c[0])
Did you get the correct answer?
Part 2 of Pop Quiz¶
# We'll change b to a[:]
a = [15, 20]
b = a[:]
c = [10, a, b]
b[1] = 2*a[0]
c[1][0] = c[0]
c[0] = a[0] + c[1][1] + b[0] + c[2][1]
print('id(a) =>', id(a))
print('id(b) =>', id(b))
print('a is b =>', a is b)
print(a)
print(b)
print(c)
The operator [:] creates a new list that is a copy of the list in a, so the ids are still different for a and b. So the results for this second scenario are exactly the same as for the first scenario.
Part 3 of Pop Quiz¶
a = [15, 20]
b = a # replace b = [15, 20] with b = a
c = [10, a, b]
b[1] = 2*a[0]
c[1][0] = c[0]
c[0] = a[0] + c[1][1] + b[0] + c[2][1]
print('id(a) =>', id(a))
print('id(b) =>', id(b))
print('a is b =>', a is b)
print(a)
print(b)
print(c)
Since there is aliasing between a and b in this scenario, the final results are different from the previous two.
Question: What about strings? Are Strings mutable?¶
# We can use operations that work on sequences, like these:
state = 'Pennsylvania'
print(state[2])
print(state[3:7])
print('Penn' in state)
Try to change the string and see what happens:¶
state[0] = 's'
Can we append something onto the end of a string? Run the code below:¶
state.append('s')
Strings are NOT mutable, so we cannot perform mutations on them¶
10. Tuples¶
A tuple is an immutable sequence of values. It's written using parens rather than brackets.
# A homogeneous tuple of five integers
numTup = (5, 8, 7, 1, 3)
# A homogeneous tuple with 4 strings
stateTup = ('Kansas', 'Idaho', 'New Jersey', 'Louisiana')
# A pair is a tuple with two elements
pair = (7, 3)
# A tuple with one element must use a comma to avoid confusion with parenthesized expression
singleton = (7, )
# A tuple with 0 values
emptyTup = ( )
# A heterogeneous tuple with three elts
heterogeneousTuple = (42, 'Hello', False)
On tuples we can use any sequence operations that don't involve mutation:
len(stateTup)
stateTup[2]
stateTup[1:3]
'Missouri' in stateTup
stateTup*2 + ('Arkansas',)
However, any sequence operation that tries to change a tuple will fail
stateTup[0] = 'North Dakota'
stateTup.append('Maine')
stateTup.pop(3)
11. Tuple Assignment¶
Consider an information tuple with three parts: (1) name of class (2) number of students (3) fulfills MM
classInfo = ('CS111', 24, True)
We can extract name parts of this tuple using three assignments:
name = classInfo[0]
numStudents = classInfo[1]
isMM = classInfo[2]
print('Name of Class:', name, '| Number of Students:', numStudents, '| Fulfills MM Requirement:', isMM)
But it's simpler to extract all three parts in one so-called tuple assignment:
(name, numStudents, isMM) = classInfo
print('Name of Class:', name, '| Number of Students:', numStudents, '| Fulfills MM Requirement:', isMM)
Also note that parens are optional in a tuple assignment, so this works, too:
name, numStudents, isMM = classInfo
print('Name of Class:', name, '| Number of Students:', numStudents, '| Fulfills MM Requirement:', isMM)
12. Optional: Enumerations¶
An enumeration pairs an index with each element of a sequence.
enumerate('boston') # An enumeration is an abstract value
list(enumerate('boston')) # Use list() to show the pairs in an enumeration
list(enumerate([7, 2, 8, 5]))
It's handy to loop over the (index, value) pairs in an enumeration.
for (i,char) in enumerate('boston'): # i and char are names for parts of each pair
print(i, char)
The above shows that tuple assignment works for for loops, too!