CS111 Lecture: Functions¶
The content of this notebook will be covered over three three lectures. There is no need to try to complete it at right away.
Table of Content
1. Defining your own functions
2. Multiple parameters
3. Excercise 1: write your own function average
4. Functions that call other functions
5. Zero-parameter functions
6. return vs. print
7. Functions with side effect and no return value
8. Exercise 2: Incremental development of functions with number statistics
9. Exercise 3: Old Macdonald has a farm
10. Functions with graphics
11. Exercise 4: Colorful stars
12. Exercise 5: drawRectangle
13. Exercise 6: drawSquare
14. Fish Tank
15. Fruitful Graphics
16. Exercise 7: Fruitful square
17. Practice writing functions
1. Defining your own functions¶
Functions are a way of abstracting over computational processes by capturing common patterns. You have already used built-in functions like len, max, input and many more. Here is a user-defined function to compute the square of a number.
def square(x):
"""A simple user-defined function."""
return x * x
Calling or invoking the function: we can call a function many times, but we define it once.
square(5)
square(7.5)
Parameters
A parameter is a variable used in the definition of a function, which will be initialized with an argument value during a function call.
The particular name we use for a parameter is irrelevant, as long as we use the name consistently in the function's body.
def square(someNumber):
"""A similar definition of the function, but using a different parameter name."""
return someNumber * someNumber
The following function call will generate the same result as the one from the definition of the function with a different parameter name.
square(5)
2. Multiple parameters¶
A function can take as many parameters as needed. They are listed one by one, separated by comma.
Important: The order of parameters specifies the order of argument values used during the function call.
def energy(mass, velocity):
"""Calculate kinetic energy"""
return 0.5 * mass * velocity**2
Problem description: A 1 kg brick falls off a high roof. It reaches the ground with a velocity of 8.85 m·s-1. What is the kinetic energy of the brick when it reaches the ground?
Call the function:
energy(1, 8.85)
import math
def distanceBetweenPoints(x1, y1, x2, y2):
"""Calculate the distance between points """
return math.sqrt((x2-x1)**2 + (y2-y1)**2)
You are given the following simple graph that depicts two points A and B in the 2-D coordinate system, where every tick is a unit of 1. Call the functioon distanceBetweenPoints with the right values to calculate the distance.
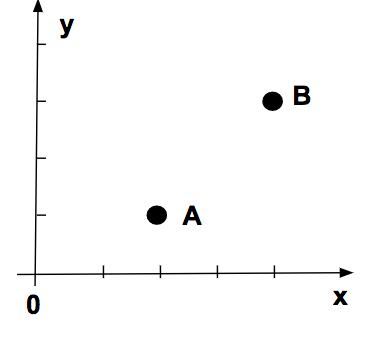
Call the function:
#Your code here
distanceBetweenPoints(2, 1, 4, 3)
3. Exercise 1: Write your function: average¶
Define a function named average that takes two numbers and returns the average of the two.
# Your code here
def average(num1, num2):
return (num1 + num2)/2
Now try calling your function as below:
average(4, 5)
average(10, 12)
4. Functions that call other functions¶
When defining your functions, you can call other functions within the body of your definition.
def favNum(name, num):
return name + "'s favorite number is " + str(num)
favNum('Andy', 4)
favNum('Ada', 17)
We can also call our own user-defined functions like the function square above. Make sure that square above is defined before you try and invoke hypotenuse.
import math
def hypotenuse(a, b):
return math.sqrt(square(a) + square(b))
hypotenuse(3, 4)
hypotenuse(5, 12)
5. Zero-Parameter Functions¶
Sometimes it's helpful to define functions that have zero parameters.
Note: you still need parentheses after the function name when defining and invoking the function.
def rocks():
return "CS111 rocks!"
print(rocks(), rocks(), rocks())
# Invoke the same function multiple times
def rocks3():
return rocks() + ' ' + rocks() + ' ' + rocks()
print(rocks3(), rocks3(), rocks3())
Python has some useful built-in functions that take zero parameters, like random.
from random import random
random()
6. return vs. print¶
returnspecifies the result of the function invocationprintcauses characters to be displayed in the shell.
def square(x):
return x*x
def squarePrintArg(x):
print('The argument of square is ' + str(x))
return x*x
def printSquare(a):
print('square of ' + str(a) + ' is ' + str(square(a)))
Try out the result of the following expressions:
square(3) + square(4)
squarePrintArg(3) + squarePrintArg(4)
printSquare(5)
IMPORTANT: If a function doesn't return a value (but only prints one as a side effect), don't use it in expressions where
a value is expected. Can you guess what result you'll get below:
printSquare(3) + printSquare(4)
DIGGING DEEPER: See the notes on the None value and the NoneType type to understand in more detail why this happens.
We can verify that None is not a string, by invoking the built-in function type:
type(None)
type(printSquare(3))
result = printSquare(3)
print(result)
7. Functions with side effect and no return value¶
A function doesn't always need to return a value. It might only display characters on the screen, or perform other side effects.
def printBanner(s):
# 5 stars, 3 spaces, input string, 3 spaces, 5 stars
banner_length = 5 + 3 + len(s) + 3 + 5
print('*' * banner_length)
print('*****' + ' ' + s + ' ' + '*****')
print('*' * banner_length)
printBanner("CS111")
The following printTimeFromSeconds function use arithmetic operations and local variables to display the time for a given number of seconds.
def printTimeFromSeconds(s): # Total seconds
seconds = s % 60 # Remaining seconds
m = s // 60 # Total minutes
minutes = m % 60 # Remaining minutes
h = m // 60 # Total hours
hours = h % 24 # Remaining hours
days = h // 24 # Total days
print(str(s) + ' seconds is equivalent to:')
print(str(days) + ' days')
print(str(hours) + ' hours')
print(str(minutes) + ' minutes')
print(str(seconds) + ' seconds')
printTimeFromSeconds(1000000)
8. Exercise 2: Incremental Development of Functions with Number Statistics¶
Incremental development is the process of slowly adding bits of code in a cumulative fashion and testing along the way to ensure proper functionality. We will illustrate incremental development using a function that prints out statistics about a number, similar to PS01.
Our function should take a single parameter called num and print out some simple statistics about the number. Below is an example output when our function is given the number three.
Your number is 3.
Your number squared is 9.
Your number has a remainder of 1 when divided by 2.
In the box below, focus on the header definition and simply have the function print out three and nothing else. It's always important to start simple.
# create a function called numStats that takes a parameter called num and prints it out
# Your code here
def numStats(num):
print(num)
Test to make sure your function properly works by calling it in the box below.
# Call your function and make sure it produces the right output
numStats(3)
Adjust the body of the function so that it now prints out the first line of text.
# Your code here
def numStats(num):
print("Your number is", num)
Test to make sure your function properly prints the first line by calling it in the box below.
numStats(3)
Add to the body of your function by printing out second line of text.
# Your code here
def numStats(num):
print("Your number is", num)
print("Your number squared is", num**2)
Test to make sure your function properly prints the first two lines by calling it in the box below.
numStats(3)
Complete the function by adding to the body of your function so that it prints the final line.
# Your code here
def numStats(num):
print("Your number is", num)
print("Your number squared is", num**2)
print("Your number has a remainder of", num%2, "when divided by 2")
Test to make sure your function properly works.
numStats(3)
Incremental development is a key tool for writing code, especially complex code! We will employ this strategy as the semester progresses and we learn more cool coding concepts.
9. Exercise 3: Old Macdonald's Song¶
Write a function named verse to generate verses of the song, Old MacDonald had a farm.
What should the function parameters be?
Old MacDonald had a farm, EE-I-EE-I-O,
And on that farm he had a cow, EE-I-EE-I-O,
With a moo moo here and a moo moo there
Here a moo, there a moo, everyone a moo moo
Old MacDonald had a farm, EE-I-EE-I-O.
Old MacDonald had a farm, EE-I-EE-I-O,
And on that farm he had a chicken, EE-I-EE-I-O,
With a cluck cluck here and a cluck cluck there
Here a cluck, there a cluck, everyone a cluck cluck
Old MacDonald had a farm, EE-I-EE-I-O.
Old MacDonald had a farm, EE-I-EE-I-O,
And on that farm he had a horse, EE-I-EE-I-O,
With a neigh neigh here and a neigh neigh there
Here a neigh, there a neigh, everyone a neigh neigh
Old MacDonald had a farm, EE-I-EE-I-O.
Old MacDonald had a farm, EE-I-EE-I-O,
And on that farm he had a sheep, EE-I-EE-I-O,
With a baa baa here and a baa baa there
Here a baa, there a baa, everyone a baa baa
Old MacDonald had a farm, EE-I-EE-I-O.
# Flesh out the definition for the function verse
def verse(animal, noise):
"""Writes a verse of five lines for the Old Macdonald song."""
print('Old MacDonald had a farm, EE-I-EE-I-O,')
print('And on that farm he had a ' + animal + ', EE-I-EE-I-O,')
# Your code here - complete this function body
twoNoise = noise + ' ' + noise
print('With a', twoNoise, 'here and a', twoNoise, 'there')
print('Here a', noise + ",", 'there a', noise + ", everyone a", twoNoise)
print('Old MacDonald had a farm, EE-I-EE-I-O')
Test your function below to generate a few different verses.
verse('cow', 'moo')
verse('chicken', 'cluck')
verse('horse', 'neigh')
10. Functions with Graphics¶
We can also use functions to help us easily implement turtle graphics. But first let's motivate the need for functions. Here is a turtle picture below that makes three stars. Remember to first import the necessary turtle modules.
from turtle import *
from turtleBeads import *
reset()
setupTurtle()
teleport(0, 100)
rt(72)
fd(100)
rt(144)
fd(100)
rt(144)
fd(100)
rt(144)
fd(100)
rt(144)
fd(100)
rt(72)
teleport(200, 100)
rt(72)
fd(200)
rt(144)
fd(200)
rt(144)
fd(200)
rt(144)
fd(200)
rt(144)
fd(200)
rt(72)
teleport(-200, 100)
rt(72)
fd(200)
rt(144)
fd(200)
rt(144)
fd(200)
rt(144)
fd(200)
rt(144)
fd(200)
rt(72)
While the above code works perfectly well, it's rather long and repetitive. How can we use functions to abstract away the similar elements between these three stars but still capture their differences? First think about what is similar:
- All of the code above uses the same right turns
- All move forward by the same amount within each star
- All begin by teleporting to the location of the topmost point of the star
Now consider what is different:
- The starting location
- the length of each side of the star is different
Key idea: The body of a function should capture the similarities amongst code and the parameters should express the differences.
def star(startX, startY, length):
teleport(startX, startY)
rt(72)
fd(length)
rt(144)
fd(length)
rt(144)
fd(length)
rt(144)
fd(length)
rt(144)
fd(length)
rt(72)
To test out our brand new function, first clear and reset the turtle screen
reset()
setupTurtle()
Now let's make three function calls using our new function. Note that these functions do not need to return a value because we are simply drawing the graphics.
star(0, 100, 100)
star(200, 100, 200)
star(-200, 100, 200)
Our star example is a great instance of the power of abstraction. Remember that abstraction is the process of hiding inner details and capturing essential similarities. Here the implementation of our function captures what is similar among all five-pointed stars and wraps those details in a function. The contract of the function allows the users to pass arguments to express the differences among stars.
You may notice some repetition within the function star, in particular the repeated calls to fd(length) and rt(144). We can reduce this repetition through iteration. We will get there in a few weeks!
11. Exercise 4: Colorful Stars¶
Suppose we want to be able to change the pen color for each star so the outline is a different color. How should we amend our function to capture this difference? You can change the pencolor with the function pencolor(color) where color is the color of the pen as a string. Write your answer below.
def colorfulStar(startX, startY, length, color):
# Your code here
pencolor(color)
teleport(startX, startY)
rt(72)
fd(length)
rt(144)
fd(length)
rt(144)
fd(length)
rt(144)
fd(length)
rt(144)
fd(length)
rt(72)
end_fill()
reset()
setupTurtle()
speed(3) # help see your turtle draw in a slower speed
colorfulStar(-100, 100, 100, 'red')
colorfulStar(100, 100, 100, 'blue')
colorfulStar(100, -100, 100, 'grey')
colorfulStar(-100, -100, 100, 'cyan')
12. Exercise 5: drawRectangle¶
You have been using the python module turtleBeads.py. It was developed by our lab instructor Peter Mawhorter. Let's try and implement some of the functions provided to you by turtleBeads.py.
Right now turtleBeads.py has a function called drawRectangle which draws a centered rectangle about the location of the turtle of height height and width width.
Below write your own implementation of drawRectangle. Note you will want to use penup and pendown since the rectangle needs to be centered about the starting position of the turle.
def drawRectangle(width, height):
# Your code here
penup()
lt(90)
fd(height/2)
rt(90)
bk(width/2)
pendown()
fd(width)
rt(90)
fd(height)
rt(90)
fd(width)
rt(90)
fd(height)
rt(90)
penup()
fd(width/2)
rt(90)
fd(height/2)
lt(90)
pendown()
Test your code below.
reset()
setupTurtle()
drawRectangle(300, 400)
13. Exercise 6: drawSquare¶
turtleBeads.py also provides a very similar function to drawRectangle(width, height) called drawSquare(size). drawSquare is self-explanatory. It is a function that draws a square centered around the current location of the turtle. Below implement drawSquare. Be judicious though. How is a square similar to a rectangle? Can you use something you've already created to implement drawSquare?
def drawSquare(size):
# Your code here
drawRectangle(size, size)
Test your code below.
reset()
setupTurtle()
drawSquare(300)
14. Fish Tank¶
Below is some code to draw a fish with a yellow body, black eye, and a green tail.
def staticFish():
# Make the body by drawing a yellow elipses
fillcolor("yellow")
begin_fill()
drawEllipse(50, 2) # 50 is radius and 2 is aspect ratio (makes it wider horizontally and thinner vertically)
end_fill()
# Make the eye by drawing a black circle to the upper right of the ellipse
penup()
fd(50)
lt(90)
fd(15)
rt(90)
pendown()
fillcolor("black")
begin_fill()
drawCircle(10)
end_fill()
# Make the tail by drawing a green triangle on the left sideof the ellipse
penup()
rt(90)
fd(15)
rt(90)
fd(150)
lt(180)
pendown()
fillcolor("green")
begin_fill()
rt(150)
fd(65)
rt(120)
fd(65)
rt(120)
fd(65)
lt(30)
end_fill()
# return the turtle back to the original starting point
penup()
fd(100)
pendown()
reset()
setupTurtle()
staticFish()
Our function is rather limited in that it always draws the same fish in the exact same position and orientation. How can we expand our fish function to make it more flexible for drawing different kinds of fish? First, let's identify some characteristics that should be different among fish?
- Body color
- Tail color
- Starting location
- Angle
- Size
What should be similar for all fish? Well it should be made of an ellipse, circle, and triangle and all of those pieces should still be proportional to each other. Below, amend the function header for fish below to capture these five differences and then implement each of the differences we stated above. Work incrementally! I suggest going in the order stated in our list above.
def fish(bodyColor, tailColor, x, y, scale, angle):
# Your code here
teleport(x, y)
lt(angle)
fillcolor(bodyColor)
begin_fill()
drawEllipse(50*scale, 2)
end_fill()
penup()
fd(50*scale)
lt(90)
fd(15*scale)
rt(90)
pendown()
fillcolor("black")
begin_fill()
drawCircle(10*scale)
end_fill()
penup()
rt(90)
fd(15*scale)
rt(90)
fd(150*scale)
lt(180)
pendown()
fillcolor(tailColor)
begin_fill()
rt(150)
fd(65*scale)
rt(120)
fd(65*scale)
rt(120)
fd(65*scale)
lt(30)
end_fill()
penup()
fd(100*scale)
pendown()
rt(angle)
Below test your code. You should have a very pretty fish tank with different fish.
def drawCanvas(width, height, color):
teleport(0, 0)
fillcolor(color)
begin_fill()
drawRectangle(width, height)
end_fill()
# Picture
reset()
setupTurtle()
drawCanvas(800, 800, "cyan")
fish("yellow", "green", -175, 200, 1.5, 45)
fish("blue", "red", 100, 100, 0.5, -45)
fish("purple", "blue", -200, -200, 1, 0)
fish("orange", "purple", 150, -150, 1.5, -60)
One important point to note. A key aspect that made amending the staticFish function much less laborious was that the function didn't rely on teleport() to move the turtle from shape to shape. Why was that helpful? Changing the angle of the entire fish becomes much more complex if you need to recalculate the x and y coordinates of each teleport to account for the angle.
15. Fruitful Graphics¶
We say that a function is fruitful if it returns a value. If a function does not return a value, then we say the function is not fruitful. Technically, functions without return do in fact return None but None serves as a placeholder to represent nothing. All of the above graphic functions we have worked with have not been fruitful. They draw pictures, which are side-effects, but do not return anything. Let's now make some fruitful turtle graphics that return key statistics about the pictures drawn.
Here is a simple example below that draws a triangle.
def triangle(size):
rt(60)
fd(size)
rt(120)
fd(size)
rt(120)
fd(size)
rt(60)
reset()
setupTurtle()
triangle(50)
Suppose we wanted to draw a triangle but also return the perimeter. We can add to the function above by simply returning the perimeter at the end.
def trianglePlusPerimeter(size):
rt(60)
fd(size)
rt(120)
fd(size)
rt(120)
fd(size)
rt(60)
return size * 3
reset()
setupTurtle()
trianglePlusPerimeter(50) # should return 150
16. Exercise 7: Fruitful Square¶
Below write a function that draws a square of side size and returns the perimeter of the square. Unlike the drawSquare function from turtleBeads.py, let's not center the square around the starting point for simplicity. Instead the starting point should be the upper left corner of the square.
def squarePlusPerimeter(size):
# Your code here
fd(size)
rt(90)
fd(size)
rt(90)
fd(size)
rt(90)
fd(size)
rt(90)
return size * 4
Test your code below. It should return 400.
reset()
setupTurtle()
squarePlusPerimeter(100)
Now that we have two functions that can return perimeter, it becomes easy to get the perimeter of a canvas of shapes.
reset()
setupTurtle()
totalSize = 0
pu()
bk(200)
pd()
totalSize += trianglePlusPerimeter(50)
pu()
fd(75)
pd()
totalSize += squarePlusPerimeter(50)
pu()
fd(125)
pd()
totalSize += trianglePlusPerimeter(50)
pu()
fd(75)
pd()
totalSize += squarePlusPerimeter(50)
pu()
fd(125)
pd()
totalSize += trianglePlusPerimeter(50)
print(totalSize)
17. Practice Writing Functions¶
Pick one of the following and write a new function. It's good to have practice translating the English description into Python.
A. squareDiff¶
Write a function called squareDiff that takes two numbers and returns the positive difference between their squares (you can use abs()).
squareDiff(4, 3) returns 7; squareDiff(5, 11) returns 96.
thon.
# Your code here
def squareDiff(x, y):
return abs(x*x - y*y)
# Test your squareDiff function here
print(squareDiff(10, 5)) # should print 75
print(squareDiff(4, 3)) # should print 7
print(squareDiff(5, 11)) # should print 96
B. lottery¶
Given a function lucky() that returns a random integer between 1 and 100, write a function called lottery that will print 3 random lottery numbers with each number separated by a space.
For example, lottery() might print 57 81 41.
import random
def lucky():
'''Returns a random integer between 1 and 100, inclusive'''
return random.randint(1,100)
# Your code here
def lottery():
print(lucky(), lucky(), lucky())
lottery()
lottery()
C. greeting¶
Write a function called greeting that asks for a user’s name using input(), and then prints a personalized greeting. E.g. Please tell me your name: Joyce
“Hi Joyce, hope you’re having a great day!” or something similar.
# Your code here
def greeting():
'''Prints a friendly personalized greeting after
asking for the person's name'''
name = input('Please tell me your name: ')
print('Hellooooooo '+name+'! So glad to see you!')
greeting()
greeting()
D. splitSquare¶
Write a function called splitSquare that takes 2 colors and draws a size square using turtleBeads, where the left half is filled with one color, and the right half with the other color. For example, here is the picture drawn when we call splitSquare(100, 'black', 'orange'):

import turtle
from turtleBeads import *
# Your code here
def splitSquare(size, c1, c2):
'''Draws a square of size with the left half color c1
and the right half color c2'''
pencolor(c1)
fillcolor(c1)
leap(-size/4)
# draw the left half of the square, which is a rect
begin_fill()
drawRectangle(size/2, size)
end_fill()
leap(size/2)
pencolor(c2)
fillcolor(c2)
# draw the right side of the square
begin_fill()
drawRectangle(size/2, size)
end_fill()
leap(-size/4)
reset()
setupTurtle()
splitSquare(100, 'red','pink')