Lab 7.

Our plan for today

  • sumUpTo
  • exponents
  • fruitful recursion with lists of strings
  • fruitful recursive hearts in cs1graphics (because we love python!)
  • fruitful recursive turtle graphics
Download the lab7_programs folder from the cs111d download directory. Rename it so it contains your name, and save all your files from today's lab in that folder. In today's lab, you'll practice writing fruitful recursive functions. We will start with numbers and lists, and then move to cs1graphics and turtles. We'll produce cool patterns using cs1graphics and also in TurtleWorld. Remember that your cs1graphics files will need 
from cs1graphics import *
For your turtle world code, you can use turtles.py in the lab7_programs folder as a template to get you started (you won't need this until Task 4). Task 0: Fruitful recursion: sumUpTo Create a new file in your lab7_programs folder and name it something descriptive (e.g. lab7.py). In this new file, create a fruitful recursive function called sumUpTo(num) that will return the sum of all numbers up to and including the given number. For example, 
sumUpTo(0) returns 0
sumUpTo(3) returns 6 (because 3 + 2 + 1 = 6)
sumUpTo(10) returns 55
sumUpTo(88) returns 3916
sumUpTo(500) returns 125250
sumUpTo(1000) returns "RuntimeError: maximum recursion depth exceeded"
Make sure that your function actually returns a value (as opposed to merely printing it). Here's a way to test it. If a line in your lab7.py file says this: 
print sumUpTo(10)
That should produce the number 55. If it produces "None", then your function prints rather than returns the value. Task 1: Fruitful recursion: exponents In your lab7.py file, create a fruitful recursive function called exp(base,power) that will return basepower. For example, 
exp(6,0) ==> 1
exp(2,5) ==> 32
exp(9,2) ==> 81
exp(5,11) ==> 48828125
exp(4,-2) ==> This function handles positive exponents only
Task 2: Fruitful recursion: String lists Write a function called mapO that takes a list of strings, and returns a list of strings with an 'o' added to the end of each string. Here are some examples: 
print mapO(['hell','cheeri','JL','ore']) 
print mapO([])
print mapO(['No','Yes','Maybe'])
print mapO(['Robert','Carl','Leonard','Rome','Valentin'])
produces 
['hello', 'cheerio', 'JLo', 'oreo']
[]
['Noo', 'Yeso', 'Maybeo']
['Roberto', 'Carlo', 'Leonardo', 'Romeo', 'Valentino']
Task 3: Fruitful recursion: Dropping R words Write a function called dropRs that takes a list of strings, and returns a list where all the strings starting with the letter 'r' have been removed. 
print dropRs(['snow','rain','sleet','turtles'])
print dropRs(['Swim','Bike','Run'])
print dropRs(['lather','rinse','repeat'])        
print dropRs(['read','write','rithmetic'])
print dropRs(['red','room','really'])
produces 
['snow', 'sleet', 'turtles']
['Swim', 'Bike']
['lather']
['write']
[]
Task 4: Fruitful recursion with cs1graphics We have used the cs1graphics package a lot in this course, but this is the first time we will write fruitful recursive functions using cs1graphics. The key is that our fruitful recursive functions will return a layer, and that layer will contain the object to be drawn on the cs1graphics canvas.

In your lab7_programs folder, there is a file called hearts.py. Inside this file is a function called makeHeart(size,color) that creates and returns a layer with a heart shape with the given size and color. Note that size is the radius of the semicircles on top of the heart.
Here are some sample invocations of makeHeart(size,color): 

paper0 = Canvas(500,500,'ivory','makeHeart demos')
h1 = makeHeart(100,'pink')
h1.moveTo(200,200)
paper0.add(h1)  
h2 = makeHeart(50,'orange')
h2.moveTo(390,305)
paper0.add(h2)
h3 = makeHeart(30,'navy')
h3.moveTo(90,370)
paper0.add(h3)

Note how first the makeHeart() function is called, and then the resulting layer is assigned to a variable (e.g. h1, h2 or h3 in the code above). Let's consider the variable h1. See how h1 is moved toward the center of the canvas (200,200) (the exact center would be (250,250))? This is important. If we executed this code (without the move), this is what we would see: 
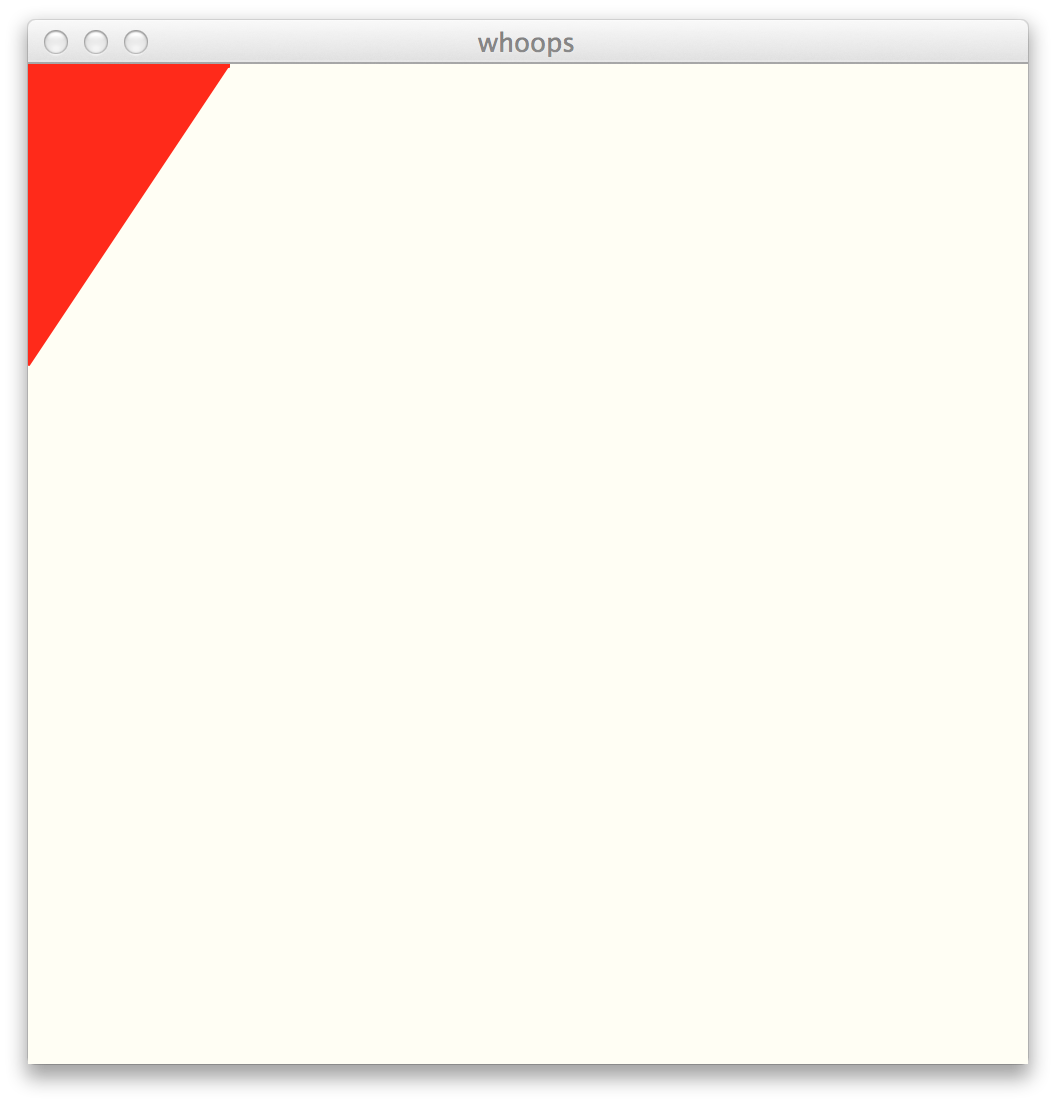
paper = Canvas(500,500,'ivory','whoops')
h1 = makeHeart(100,'red')
paper.add(h1)

Why? Because the makeHeart() function returns a layer that contains a heart that is centered around the Point(0,0), the default center point for all cs1graphics objects. If we do NOT move the layer, then it remains in the original position, which is why we can only see the lower right hand side of the heart.

Task 4a: return a row of hearts recursively Write a function called heartRow(number,size,color) that returns a row of number hearts that have size size and are color color. In this function, it is the number of hearts that controls the recursion. For example, heartRow(0,10,'red') would not produce any hearts. Note that heartRow() is fruitful in that it returns a row of hearts. We'll use this function in the next task.
Below are some sample invocations of heartRow(number,size,color)

Task 4a extra: return a "star" of rows of hearts For this task, assume that each of the 8 "petals" will be separated by 45 degrees. You should call heartRow() to generate the rows of hearts, and then add each row to the Layer that starBurst returns. Below are some sample invocations of starBurst(numPetals,number,size,color)

starBurst(8,10,15,'red')

starBurst(8,3,40,'orange')


Task 4b: Return a row of FADING hearts recursively Write a function called fadingHeart(size,color) that returns a row of decreasing sized hearts that have the color color. Note that in this task, the recursion is controlled not by an explicit count (as it was above in heartRow(), but rather by the size of the current heart. Important notes for your code:
  1. Your fadingHeart function will only draw hearts if the size is greater than 10
  2. Each successive heart is 20% smaller than previous one
  3. Each heart is moved to the right a fixed distance of 20 from the previous one
Below are some sample invocations of fadingHeart(size,color)

Task 4c: return a row of NESTED hearts recursively Write a function called nestedHeart(size,color1,color2) that returns a row of decreasing sized hearts that have alternating color color and are nested on top of each other. Important notes for your code:
  1. Your nestedHeart function will only draw hearts if the size if greater than 10
  2. Each successive heart is 20% smaller than previous one
  3. The hearts must alternate colors between color1 and color2 (otherwise, it is hard to see them, since if they were all the same color they would blend together)
In the image below, the two leftmost hearts are examples of nestedHeart(): 
paper2 = Canvas(800,500,'white','Nested heart variations')
nestH = nestedHeart(200,'red','thistle')
paper2.add(nestH)
nestH.moveTo(300,200)
nestH2 = nestedHeart(35,'lemonchiffon','navy')
paper2.add(nestH2)
nestH2.moveTo(450,400)


Task 4c extra: count the total number of hearts drawn nestedHeart() is a fruitful recursive function that returns a layer containing the nested hearts. Copy your nestedHeart() function and rename the new version nestedHeartCount(). Remember that a python function can return multiple values, and those values can be different types. Here are some sample invocations of nestedHeartCount(). 
nestH, count = nestedHeartCount(200,'red','thistle')
print count  
# the line above should print 15 
nestH2, count2 = nestedHeartCount(35,'lemonchiffon','navy')
# the line above should print 7
Task 5: Squares with clipped corners Now we're switching gears and moving to turtle world. Our focus, however, is still on fruitful recursive functions. The fruitful recursive boxes method takes four parameters:
  1. the length of the largest square
  2. the shrink factor of the squares drawn at each of the four corners
  3. the length of an edge of the smallest outer box
  4. the color of the turtle's pen
For example, in the screenshot below, let's look closely at the upper left corner first. boxes(400, 0.4, 100, 'magenta') ,the largest box has side length of 400. In each corner, there is a smaller box drawn. Each smaller box has side length of 160 (400*0.4 = 160). There are no more boxes drawn, because the next set of corner boxes have side length 64 (160*0.4), and 64 is less than the smaller outer box length of 100

. boxes(400, 0.4, 100, 'magenta') produces a total of 5 boxes (1 outer box + 4 nested ones) and a total length of 4160. [4 smaller boxes 160 x 4 = 2560; dimensions of outer box with side length 400 = 1600; 2560 +1600 = 4160].

Several different variations are shown below.

Hints:

  1. First, write the recursive function to produce the picture
  2. After that works, then go back and add in the fruitful counting of boxes only
  3. After the counting of boxes works, add in the fruitful sum of all the lengths drawn
  4. Remember that a function can return two values by separating them with a comma like this: return x, y
  5. As a corollary, if a fruitful function returns two values, then it can be called like this: x, y = boxes(400, 0.30, 50, 'red')
boxes(400, 0.4, 100, 'magenta')
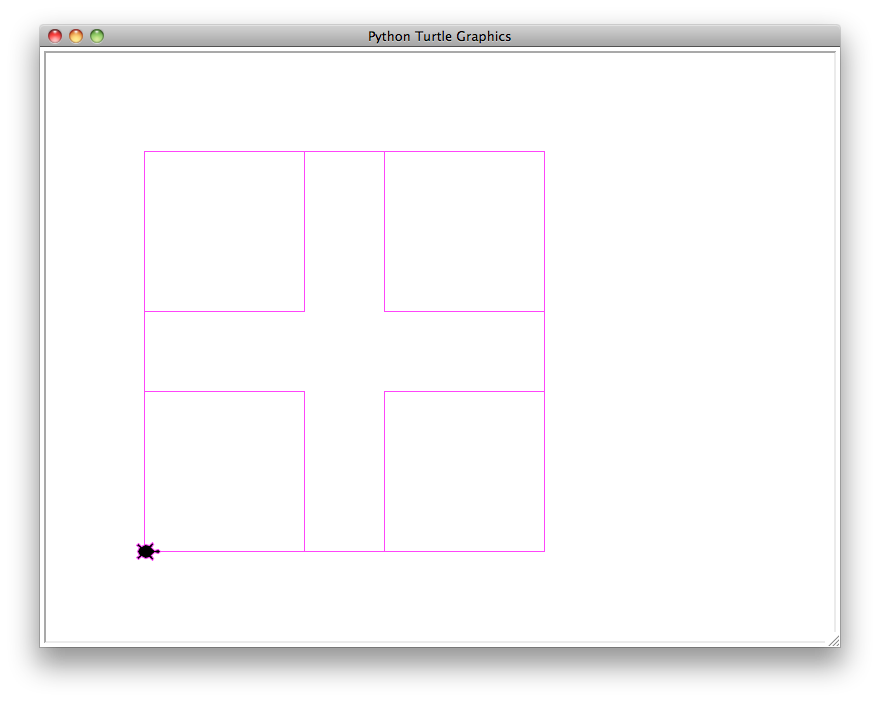5 boxes, 4160 total length of all boxes 		boxes(400, 0.33, 30, 'magenta')
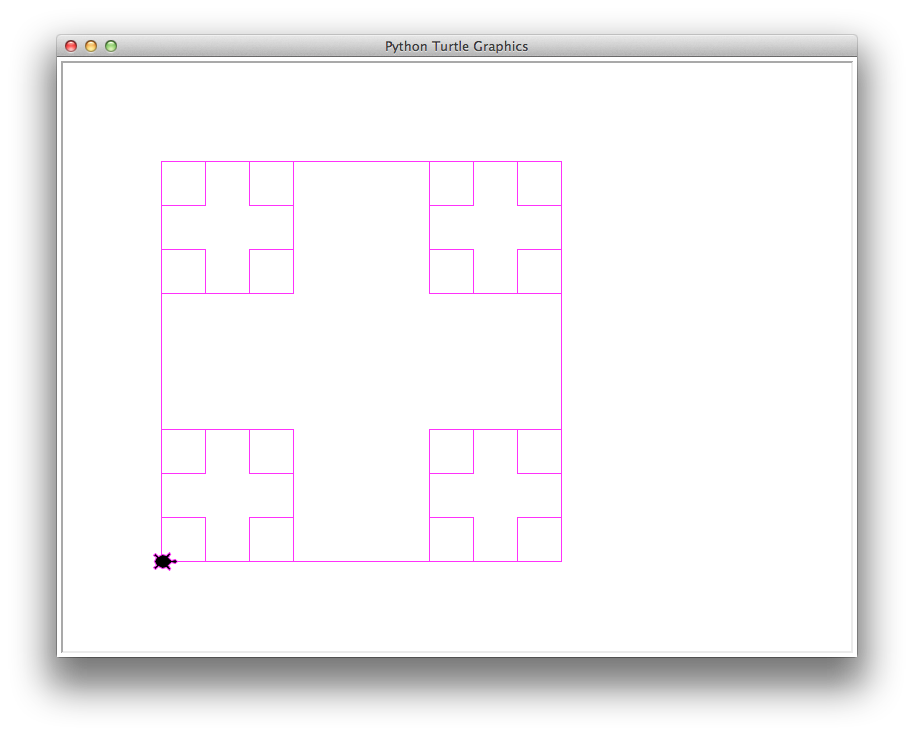21 boxes, 6499.84 total length of all boxes
boxes(400, 0.25, 15, 'magenta')
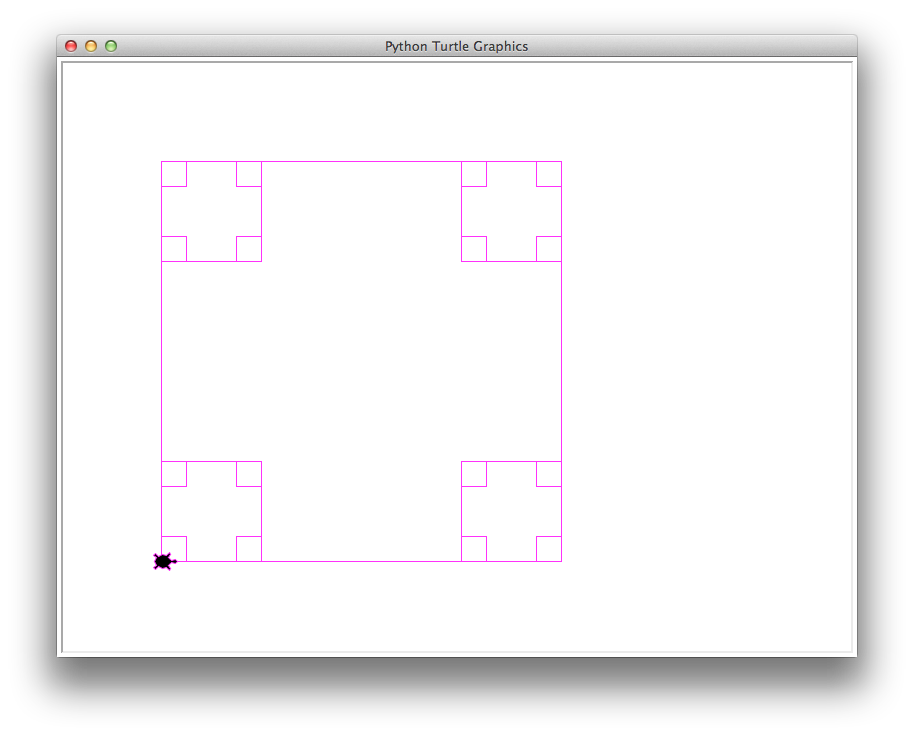21 boxes, 4800 total length of all boxes 		boxes(400, 0.4, 50, 'magenta')
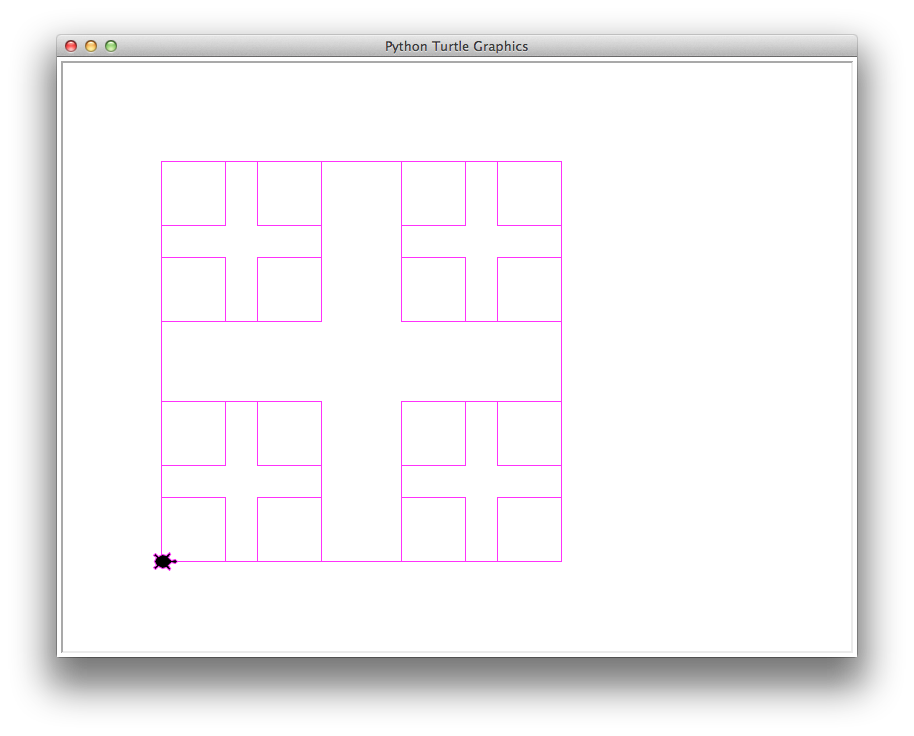21 boxes, 8256 total length of all boxes
boxes(400, 0.44, 30, 'magenta')
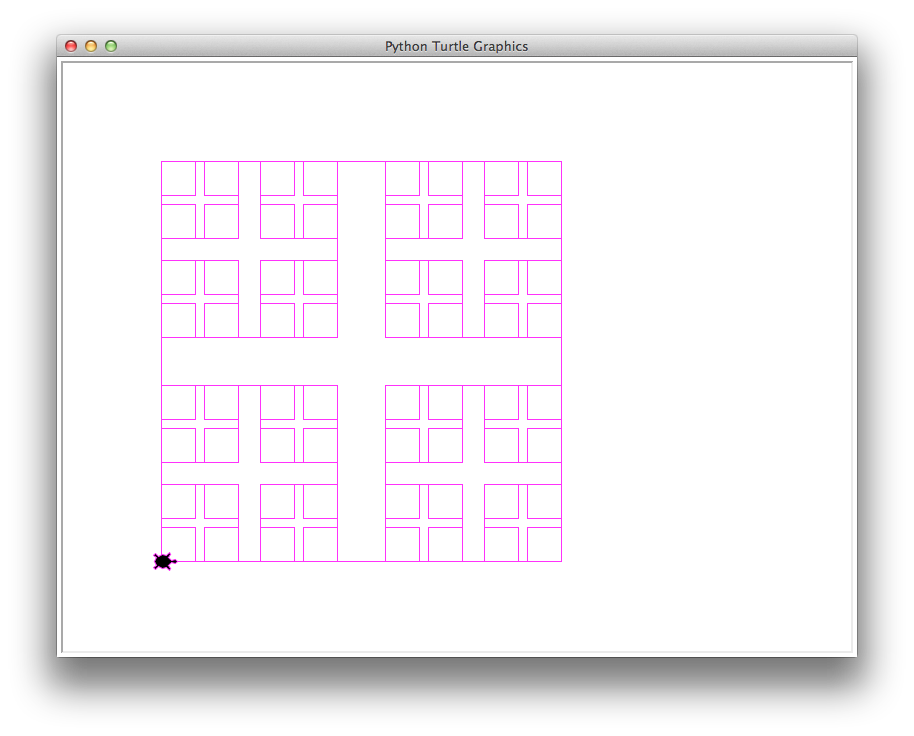85 boxes and 18095.0016 total length of all boxes 		boxes(400, 0.4, 10, 'magenta')
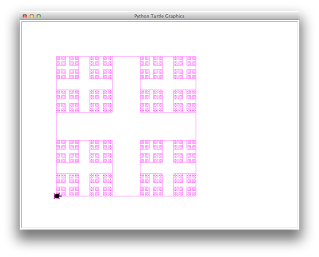1365 boxes and 42072.576 total length of all boxes
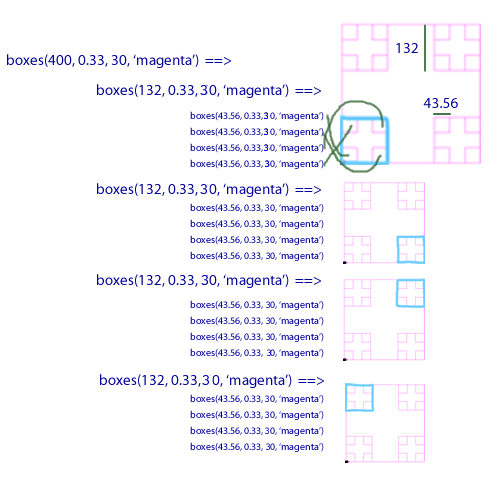
Here's a diagram that shows the flow of how the recursive method boxes invokes itself (the first image is enlarged to show detail):

If you still have time, you can experiment with more heart variations in cs1graphics below:

Task 4c extra: skew the hearts to the left Now, after your nestedHeart() works properly, think about how to create the two images on the right, which have the nested hearts, but skewed to the left. There is only one line of code that needs to be added to move each successive nested heart to the left a distance of 20% of the heart size. Here are the invocations that created the two hearts on the right in the image above: 
# testing nestedLeftHeart
nestL = nestedLeftHeart(100,'orangered1','mistyrose')
paper2.add(nestL)
nestL.moveTo(600,100)
nestL2 = nestedLeftHeart(70,'black','darkgrey')
paper2.add(nestL2)
nestL2.moveTo(600,300)
Experiment with other formulations to create intriguing pictures! Task 4d: draw a row of blasting off hearts recursively Now let's create some definitely psychedelic heart images. We'll call these sideHearts since each heart has smaller hearts coming out of its sides. Important notes for your code:
  1. sideHeart takes 3 parameters: the size of the biggest heart and the two alternating colors
  2. the sideHeart function will only draw hearts if the size if greater than 20
  3. the smaller side hearts are 1/3 the size of the big heart
  4. the small heart on the left is rotated 135 degrees from the center heart and moved a distance of size vertically and a distance of size horizontally from the center heart
  5. the small heart on the left is rotated -135 degrees from the center heart and moved a distance of size vertically and a distance of size horizontally from the center heart
  6. Each successive center heart is 25% smaller than the previous one
  7. Each triplet of hearts (center heart, smaller left heart, smaller right heart) are the same color
  8. Successive triplets alternate between color1 and color2
The image below is generated from this code: 
paper3 = Canvas(800,800,'white','sideHearts')
sideH = sideHeart(200,'slategray','red')
paper3.add(sideH)
sideH.moveTo(400,200)


The image below illustrates how the sideHeart() function produces drawings with relatively small sizes: 
# Generating another sideHeart
paper4 = Canvas(800,800,'white','More sideHearts')
sideH2 = sideHeart(100,'slategray','yellow')
paper4.add(sideH2)
sideH2.moveTo(250,200)

# 1 heart triplet
s1 = sideHeart(25,'navy','darkolivegreen')
paper4.add(s1)
s1.moveTo(300,400)

# 2 heart triplets
s2 = sideHeart(30,'navy','darkolivegreen')
paper4.add(s2)
s2.moveTo(400,400)

# 3 heart triplets
s3 = sideHeart(40,'navy','darkolivegreen')
paper4.add(s3)
s3.moveTo(520,400)

# 4 heart triplets
s4 = sideHeart(50,'navy','darkolivegreen')
paper4.add(s4)
s4.moveTo(650,400)

# 5 heart triplets
s5 = sideHeart(70,'navy','darkolivegreen')
paper4.add(s5)
s5.moveTo(400,550)