CS111, Wellesley College, Spring 2003

Problem Set 6

Due on Tuesday, March 25 by 11pm

(Extra Credit due 5pm Saturday, March 29)

About this Problem Set

The purpose of this problem set is to give you more experience with recursion and writing recursive methods that return values. Task 1 is a pencil-and-paper problem in which you will draw an invocation tree for a recursive function. In Task 2, you will use recursion in PictureWorld to generate a recursively structured quilt. In Task 3, you will use recursion in BuggleWorld to implement the elaborate buggle bagel-harvesting ritual. The code for Tasks 2 and 3 is available in the ps6_programs folder in the cs111 download directory on cs.wellesley.edu.

There are also four optional extra credit problems. In Extra Credit Challenge 1, you can use recursion to have buggles count the number of bagels in a maze. In Extra Credit Challenge 2, you can use recursion to have a turtle draw a diamond pattern and return the number of diamonds drawn. In Extra Credit Challenge 3, you can implement another recursive quilt pattern. In Extra Credit Challenge 4, you are asked to design your own recursive buggle/turtle/picture patterns. The code for the Extra Credit Challenges is available in the ps6_programs_extra folder in the cs111 download directory on cs.wellesley.edu.

In order to give you more time to work on the extra credit problems, you can turn in whatever extra credit problems you've done by 5pm Saturday, March 29. The required problems are due at the usual time: 11pm on Tuesday, March 25.

How to turn in this Problem Set

You are required to turn in both a hardcopy and a softcopy. For general guidelines on problem set submission, including how to submit a softcopy and how to check if you softcopy submission was successful, click here. Please make sure to keep a copy of your work, either on a zip disk, or in your private directory (or, to play it safe, both).

Hardcopy Submission of Required Problems

Your hardcopy packet for the required problems should consist of:
  1. The cover page;
  2. Your invocation tree diagram from Task 1;
  3. Your modified SierpinskiQuilt.java file from Task 2;
  4. Your modified HarvestWorld.java file from Task 3.
Staple these together, and slide the packet under the door of Elena's office (E127, in minifocus).

Softcopy Submission of Required Problems

Save the modified SierpinskiQuilt.java and HarvestWorld.java files in the ps6_programs folder. Submit the entire ps6_programs folder to your drop folder on the cs111 server.

Hardcopy Submission of Optional Extra Credit Problems

If you work on any of the optional extra credit problems, you should submit these in a separate packet. Your hardcopy packet for the extra credit problems should consist of:
  1. The extra credit cover page;
  2. Your modified MazeCounterWorld.java file from Extra Credit Challenge 1 (if you did this problem).
  3. Your modified DiamondWorld.java file from Extra Credit Challenge 2 (if you did this problem) .
  4. Your modified TriQuiltWorld.java file from Extra Credit Challenge 3 (if you did this problem) .
  5. Your modified MyBuggleWorld.java, MyTurtleWorld.java, and/or MyPictureWorld.java files from Extra Credit Challenge 4 (if you did this problem).
Staple these together, and slide the packet under the door of Lyn's office (E126).

Softcopy Submission of Optional Extra Credit Problems

If you complete any of the extra credit problems, submit the entire ps6_programs_extra folder to your drop folder on the cs111 server.

Task 1: Invocation Tree for a Recursive Function

Consider the following class method: 
    public static int f (int n) {
	if (n <= 2) {
	    return n;
	} else {
	    return n + f(n/2) + f(n/3);
	}
    }
Draw an invocation tree that summarizes the execution of the class method invocation f(30). Each node of the execution tree should have the form f(arg):result, where arg is the integer that is the argument of the invocation of f and result is the result of the invocation.

Keep in mind that dividing two integers in Java always returns an integer result. For example, (15/2) returns 7, (5/2) returns 2, and (5/3) returns 1.

Task 2: Sierpinski Quilts

Background

Gilda Quilter of the Built-a-Quilt company has decided to incorporate Sierpinski gasket designs into her latest line of quilts. When ordering one of her new quilts, a customer must specify two colors and a number that indicates the "level" of the Sierpinski gasket designs used in her quilts. Here are some pictures of her Sierpinski quilt designs for the colors black and cyan and level numbers ranging from 1 to 4:

sierpinskiQuilt(black,cyan,1) sierpinskiQuilt(black,cyan,2)
sierpinskiQuilt(black,cyan,3) sierpinskiQuilt(black,cyan,4)

Tragically, Gilda is an artist with no programming background (where was media arts when she went to college?), so she has to draw all her designs by hand. Since this is extremely error prone and tedious, the Built-a-Quilt company has decided to hire a Java programmer who can express Gilda's designs in Picture World. Impressed by your work on Problem Set 5, Built-a-Quilt hires you to implement the following method: 

  public Picture sierpinskiQuilt (Color c1, Color c2, int n);
  Assume that n >= 1. Returns one of Gilda's Sierpinski quilts that is 
  constructed out of n-level Sierpinski gaskets colored with c1 and c2.

When you carefully study Gilda's quilt patterns, you see that there are two auxiliary methods that would greatly simplify your task:

  1. The first auxiliary method is one that makes sierpinki gasket pictures in Picture World using two colors and a level number: 
      public Picture sierpinski (Color c1, Color c2, int n);
  Assume that n >= 1. Returns a picture of an n level sierpinski gasket whose 
  "body" has color c1 and whose "holes" have color c2. The resulting picture 
  should be a "lower left" triangle -- that is, a triangle two sides of which 
  are the left and bottom edges of the frame in which it is displayed.
    For example:

    sierpinski(black,cyan,1) sierpinski(black,cyan,2)
    sierpinski(black,cyan,3) sierpinski(black,cyan,4)

  2. The second auxiliary method is one that that makes an interesting picture out of any given "lower left" triangle: 
      public Picture triangles (Picture tri, int n);
  Suppose that tri is a "lower left" triangle and n >= 1. 
  Returns a picture whose lower left triangle is filled with tri and whose
  upper right triangle is an n-level Sierpinski gasket whose "body" is white
  and whose "holes" are filled with copies of tri.

    For example, suppose that rgTri the following lower-left triangle:

    rgTri

    3. Then here are some examples of triangles called with rgTri and various level numbers:

    triangles(rgTri,1) triangles(rgTri,2)
    triangles(rgTri,3) triangles(rgTri,4)

Your Task

Your task is to flesh out the skeletons of the sierpinski, triangles, and sierpinskiQuilt methods in the file SierpinskiQuilt.java within the SierpinskiQuilt folder. In addition to the usual methods of the PictureWorld contract, you may also use the following methods: 
  public Picture triangle (Color c); 
  Returns a "lower left" triangle filled with color c.

  public Picture rotations (Picture p); 
  Returns a picture consisting of four copies of p rotated
  around the center of the picture.

You may find it helpful to define additional auxiliary methods in order to complete your task.

Task 3: Harvest World

Note: Please read this entire problem carefully. Simply generating the correct final pattern is not enough to get full credit. Each specified method must behave as described below.

Bagels in BuggleWorld grow in fields (you knew that, didn't you?). Twice a year the Harvester buggles go out and harvest bagels so that buggles in BuggleWorld will have bagels to eat and play with throughout the year. Bagels are the most important commodity in BuggleWorld. Therefore, their harvesting procedure is quite complex and elaborate. It is described below:

Each Harvester is assigned a field of bagels to harvest. The buggle does not know the width or height of the bagel field. The buggle starts in the bottom left corner of the field and harvests bagels one row at a time (a row is a vertical column on the BuggleWorld grid). It doesn't matter if the buggle chooses to harvest the closest row first and work down to the end of the field or to walk to the end of the field and harvest rows on the way back to the beginning. Note that there are no bagels planted in the bottom horizontal row of the field. Instead, that is the path that buggles walk on to get from row to row.

Each row is harvested according to the following procedure:

The buggle harvests the bagels in the row by picking them up and counting them. It doesn't matter if the buggle picks up bagels on the way to the end of the row or picks them up coming back from the end.

The buggle stacks the bagels in a row near the path (starting from the second cell up) so that they will be able to dry (dried bagels are the best and keep fresh all year long).

The rest of the field needs to be covered with tarp (black) which preserves the field from bad weather during the non-growing season. The tarp is at the far end of the row (i.e. at the top of the BuggleWorld grid). The buggle needs to go to the end of the row and pull the tarp up to the point where the bagels are stacked. The buggle should count the number of empty spaces left in each row (spaces covered by the tarp).

While the Harvester buggles do all the work, their supervisors want to be able to quickly look at the field and see how it did. It's a bit difficult to see the entire field, so the Harvester buggle must mark each row indicating whether or not the row did well. Bad rows (fewer bagels than blank spaces) are marked red and will get more fertilizer and attention in the next growing season. Good rows (more bagels than blank spaces) are marked green. Fair rows (same number of bagels as blank spaces) are left uncolored. Each row is also tagged with the number of empty spaces (i.e. spaces covered with black tarp). See the pictures below for clarification.

Finally, the Harvester buggle must count the number of bagels harvested in the field and report that to her supervisor.

The following two pictures show the state of a field before and after the buggle has harvested it.


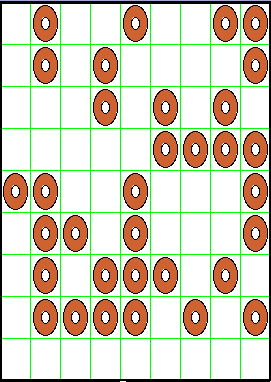Your task is to write the methods that will make the Harvester buggle do its job. You are free to write any auxiliary methods needed. At a minimum, you must define the following methods for the Harvester class. The complete specifications for each method are given in HarvestWorld.java (as usual, you can download the program files from the download directory). Each method must satisfy the specification in the code file. The descriptions below are intended to supplement and clarify the specifications in the code file.

In addition to their specificaitons, all the methods described below must also meet the following invariant:

The buggle's state (position, heading, color, and brush state) will not be changed by execution of this method. Assumes the buggle's brush is initially up.

public int harvestField()
This method assumes that the buggle is starting in the lower left corner of a field facing EAST. When this method is invoked, the buggle will harvest the field of bagels to its front and left (up to the walls in front of and to the left of the buggle) and return the number of bagels harvested in this field.

public int harvestRow()
When this method is invoked, the buggle will harvest the row of bagels to its left (i.e. the vertical column above the buggle). The number of bagels harvested in this row is returned. This method should be invoked when the buggle is facing EAST and in the bottom row (the clear path) of the field.

public int harvestBagels()
When this method is invoked, the buggle will pick up all the bagels between it and the wall and return the number of bagels picked up. This method should be invoked when the buggle is facing NORTH and in the bottom row (the clear path) of the field.

public void stackBagels(int numberBagels)
When this method is invoked, the buggle will create a stack of the specified number of bagels in front of itself. This method assumes that there will always be at least enough space in front of the buggle for the bagel stack. This method should be invoked when the buggle is facing NORTH and in the bottom row (the clear path) of the field.

public int pullTarp()
When this method is invoked, the buggle should draw a black line from the wall in front of the buggle to the current cell in front of the buggle (i.e. do not color the cell the buggle is on when the method is invoked). This method returns the number of cells colored. This method should be invoked when the buggle is facing NORTH and at the end of its bagel stack (i.e. right where the tarp should start).

public void markRow(int numberBagels, int numberSpaces)
This method paints the current cell green if numberBagels is greater than numberSpaces. The current cell is painted red if numberBagels is less than numberSpaces. The current cell is not painted if the numberBagels is equal to numberSpaces. The buggle also marks the cell with the numberSpaces (using dropInt());

Notes:

Use paintCell to color cells:
public void paintCell (Color c)
Paints the cell under this buggle with the color c

Use dropInt to drop an integer into a particular cell:
public int dropInt (int n)
Drops the integer n into the current cell and returns the integer dropped.

Test your methods by executing the HarvestWorld.html applet. When you first load the applet, the BuggleWorld grid is empty. Hit Reset to generate a bagel field. Every time you Run this applet, the number of bagels reported by the Harvester buggle will appear in the cyan box within the parameter frame window.

A working applet can be found in the test subfolder of the HarvestWorld folder. You should experiment with this test applet to better understand the behavior of Harvester buggles.

Hint: It may be easier to write the methods in the reverse order from the order listed above. That is, you might want to start by writing the markRow() method.

 

All the problems following this point are completely optional. You should only attempt them after completing the required parts of the assignment.

Extra Credit Challenge 1: MazeCounter

Before starting this problem, you should read over the notes on the PathfinderWorld example.

Maisy Buggle comes from a long line of maze-navigating buggles. But unlike other buggles, she is not satisifed with stopping when she finds the first bagel in a maze. She wants to explore the world and find out how many bagels there are in the entire maze! For instance, suppose Maisy starts at "home" (facing eastward at point (1,1)) in the following maze:

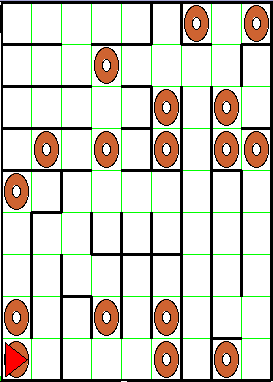
Using the same maze-navigating strategy followed by the PathFinder buggle described in the the PathfinderWorld notes, Maisy can traverse the entire maze and determine that it contains 17 bagels. Suppose that, after exploring the submaze accessible from a given cell, Maisy writes in the cell the number of bagels in that submaze. Then after she returns to her home position, the maze would be annotated as follows.

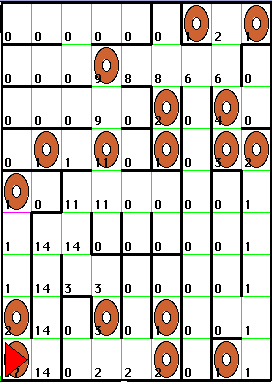
Note that the number in each cell is the number of bagels to the left, right, in front of, and under Maisy when she is in a cell (assuming she is facing the direction in which she entered the cell).

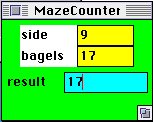
To get a better sense for how the above numbers are generated, you should experiment with the test applet MazeCounterWorld.html within the Test subfolder of the MazeCounter folder of ps6_programs_extra. This applet has a parameter window that look like this:

The numbers in yellow control the side length of the maze and the number of bagels placed randomly in the maze. If you change these and press the Reset button, a new maze will be created with these parameters. The cyan-colored box labelled result is where Maisy writes the total number of bagels in the maze when she returns home. For example, after Maisy has explored the maze depicted above, the parameter window changes to:

Before proceeding with this problem, you should play with the test applet and study the above pictures until you understand how the numbers for each cell are determined.

Maisy is a member of the MazeCounter class of buggles. Your goal in this problem is to define a collection of methods in the MazeCounter class that direct Maisy to count the number of bagels in any maze, also annotating the cells with numbers, as shown above. You should flesh out the skeleton of the MazeCounter class in the MazeCounter folder of ps6_programs_extra. This skeleton contains a "stub" version of a method with the following contract.

public int countBagels()
Counts the number of bagels to the left, right, in front of, and under this buggle.Drops this number in the cell under this buggle, and then returns it.Leaves the state of this buggle unchanged.

You should replace the stub with a method that works. As part of your solution, you should define any auxiliary methods that you find helpful. It is strongly recommended that you use a decomposition similar to the one used in for the PathFinder buggle. Your solution should work for any maze size and any number of bagels. (Warning: do not attempt to place more bagels in the maze than there are grid cells. This situation is not handled gracefully, and will cause your machine to crash.)

In order to drop an integer in a cell, you will need to invoke the following Buggle primitive:

public int dropInt (int n)
"Drops" the integer n in the cell of this buggle. The cell shows the most recently dropped integer. This method returns the integer that was dropped.

Extra Credit Challenge 2: Diamonds

Fractal Diamonds

In this problem, your job is to use recursion to draw diamond-based pictures in TurtleWorld, as shown below. The diamonds are just squares turned on end at a 45-degree angle.

side = 120, total number of diamonds is 39

side = 90, total number of diamonds is 27

side = 60, total number of diamonds is 18

side = 30,
diamonds = 8

side = 20,
diamonds = 5

side = 15,
diamonds = 4

side = 12,
diamonds = 3

side = 9,
diamonds = 2

side = 6,
diamonds = 1

Diana is a DiamondMaker, a special breed of turtles that draw these kinds of patterns based on the side length of the largest diamond. Her initial position is at the bottom corner of the largest diamond in each picture; her initial heading is east. The diamond touching the largest diamond to the right has 2/3 the side length of the largest diamond. The diamond touching the largest diamond to the left has 1/3 the side length of the largest diamond. This pattern is repeated for each new diamond drawn. The new diamond on the right is now viewed in a new orientation where the top of the new diamond is 90 degrees in a clockwise direction from the larger diamond it touches. Therefore, the "right" of this new diamond points "south" and the left of this new diamond points "north". The new diamond on the left is now viewed in a new orientation where the top of this new diamond is 90 degrees in a counterclockwise direction from the larger diamond it touches. Therefore, the "right" of this new diamond points to the "north" and the "left" of this new diamond points to the "south". Each new diamond repeats the pattern of drawing a smaller diamond on its right and a smaller diamond on its left, if possible.

Unlike other recursive turtles we have studied, Diana draws a pattern whose depth of recursion is not controlled by an explicit levels parameter. Instead, it is controlled by the fact that Diana refuses to draw any line that is less than 5 units long. For instance, in the picture where the largest diamond has a side length of 9, Diana draws the smaller easterly diamond because its side length is (2/3)*9 = 6, which is greater than 5, but she does not draw the westerly diamond because its side length would be (1/3)*9 = 3, which is less than 5.

In addition to drawing the diamonds, Diana keeps track of the total number of diamonds she has drawn in the pattern. This number is indicated for each of the sample pictures above.

Your task

Your task in this problem is to implement the following instance method in the DiamondMaker class:

public int diamonds (double side)
Draws the recursive diamond pattern described above where the side length of the largest diamond is side. Returns the number of diamonds drawn. Draws no diamond whose side length is less than 5 units long. This method meets the invariant that the turtle's state (position, heading, color, pen state) is not changed by execution of the method.

Notes:

Extra Credit Challenge 3: triQuilt

Gilda Quilter has done it again! She has designed yet another quilting pattern based on nested triangles. Examples of her pattern are shown below:

triQuilt(black,cyan,1) triQuilt(black,cyan,2)
triQuilt(black,cyan,3) triQuilt(black,cyan,4)

Your goal in this pattern is to define a triQuilt method that creates the above pictures for any given colors and levels: 

  public Picture triQuilt (Color c1, Color c2, int n);
  Assume that n >= 1. Returns one of Gilda's quilts that is 
  constructed out of triangles filled with colors c1 and c2.
  The parameter n controls the nesting level of the patterns used in the quilt.
To complete this problem, flesh out the skeleton of the triQuilt method in the TriQuiltWorld.java file within the TriQuilt folder in ps6_programs_extra. You will need to define several auxiliary methods as well. Study the patterns in the example quilts above carefully to determine what auxiliary methods you need.

Extra Credit Challenge 4: Create Your Own Recursive Patterns!

We have seen that fascinating recursive patterns can be created in BuggleWorld, TurtleWorld, and PictureWorld. In this problem, we ask you to create your own recursive patterns in one or more of these worlds.

Start with the folders MyBuggleWorld, MyTurtleWorld, and MyPictureWorld in the ps6_problems_extra folder. Feel free to define any methods you desire to create your patterns.

Some notes: