CS111, Wellesley College, Spring 2003

Problem Set 10

Due on Wednesday, May 7

THIS IS THE FINAL VERSION OF PS10, CONTAINING THE COMPLETE DESCRIPTION OF TASK 2.

Working in Pairs

On Problem Set 10, you are allowed to (but not required to) work in pairs and turn in one hardcopy and softcopy submission for both task. Programming in pairs is a fundamental aspect of an increasingly popular programming methodology known as extreme programming. Many people find that working in pairs helps both partners learn the material better and leads to clearer code with fewer bugs. Of course, there is always the danger that one partner will do most of the work and the other will learn very little; you should strive to avoid such partnerships.

If you decide to do this problem with a partner, you are required to do all Java programming side-by-side at a single computer; you are not allowed to split up the programming tasks and work on them independently. Because of this requirement, you should be careful to choose a partner whose schedule is compatible with yours. To promote interaction, you should swap "drivers" (the person who is typing at the keyboard) at regular intervals.

It is still the case that sharing of Java code is not allowed between different teams, where a "team" is either a pair of students working together or a student working alone. As always, you may discuss any aspect of the problem in English.

Reading

About this Problem Set

The purpose of this problem set is to give you experience with data abstraction, arrays, and building an interesting program from scratch. In Task 1, you will study data abstraction in the context of simple rectangle objects presented in Lecture 24. In Task 2, you will build from scratch an animation that has many BuggleWorld-like features. As an optional open-ended extra credit challenge, you can extend your implementation from Task 2 with additional features.

All code for this assignment is available in the ps10_programs folder in the cs111 download directory on the CS fileserver.

How to turn in this Problem Set

You are required to turn in both a hardcopy and a softcopy. For general guidelines on problem set submission, including how to submit a softcopy and how to check if you softcopy submission was successful, click here. Please make sure to keep a copy of your work, either on a zip disk, or in your private directory (or, to play it safe, both).

Hardcopy Submission

Your hardcopy packet should consist of:
  1. The cover page. If you have worked as a pair, be sure to list the names of both pair members and give the name of the drop folder where the softcopy can be found;
  2. Your object diagram from Task 1a;
  3. The final versions of Rect3.java, Rect4.java, and Rect5.java from Task 1b;
  4. Your object diagram from Task 1c;
  5. The final versions of GubbleWorldSprite.java, Gubble.java, GubbleGroup.java, and any other auxiliary classes that you create for Task 2.
Staple these together, and slide the packet under the door of Elena's office (E127, in minifocus).

Softcopy Submission

You should submit your final version of your ps10_programs folder. In particular,

If you have worked as a pair, you only need to submit one softcopy, in the drop folder of one of the partners. Be sure to indicate which drop folder you are using on the cover sheet of your hardcopy.

Task 1: Data Abstraction with Rects

Rects

A key idea in CS111 is data abstraction -- the notion that "users" can successfully use objects by understanding their contracts without knowing how the contracts have been implemented by the "implementers". Contracts not only serve to simplify the programming task for users, they also give implementers the flexibility to experiment with different ways to implement the same contract.

In Lecture 24, we studied the notion of multiple implementations of a data abstraction in the context of a simple rectangle abstraction known as a Rect. Conceptually, an instance of Rect is a rectangle positioned in the standard Cartesian coordinate system:

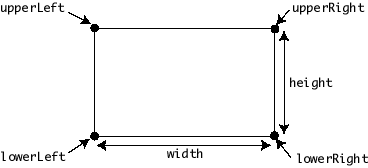
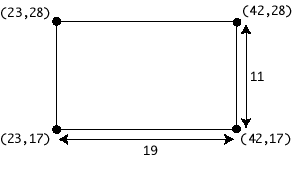
Here is a sample rectangle with lower left point (23,17), width 19, and height 11:

We emphasize that the rectangles we study in this problem are not the same as the java.awt.Rectangle class used in graphics applications, such as the Faces problem in Problem Set 9.

Below is a simple contract for the Rect class that supports two constructor methods and four instance methods. This class could easily be extended with more methods, such as methods for finding the perimeter or area of a rectangle, or returning its upper left and lower right points. But we've kept the contract small for simplicity's sake.

Rect Contract

Constructor Methods

public Rect (int llx, int lly, int width, int height);
Construct a rect from with lower left point (llx,lly), width width, and height height.

public Rect (Point ll, Point ur);
Construct a rect with lower left point ll and upper right point ur.

Instance Methods

public int width ();
Returns the width of this rect.

public int height ();
Returns the height of this rect.

public Point lowerLeft ();
Returns the lower left point of this rect.

public Point upperRight ();
Returns the upper right point of this rect

As an example, the rectangle depicted above could be created by either of the following constructor method invocations:

new Rect(23, 17, 19, 11);
new Rect(new Point(23, 17), new Point(42, 28));

In the remainder of this problem, you will consider five different implementations of the Rect contract. In order to be able to discuss the different implementations, we will name them Recti, where i ranges between 1 and 5.

Task 1a

Below are the implementations of classes Rect1 and Rect2 that implement the contract for Rect (modulo the change in constructor name). In this subtask, you should draw an object diagram that shows the result of the following sequence of statements: 
Point p1 = new Point (1,2);
Point p2 = new Point (9,6);
Rect1 a1 = new Rect1 (p1,p2);
Point ur1 = a1.upperRight();
Rect1 b1 = new Rect1 (ur1.y, ur1.x, a1.height(), a1.width());
Rect2 a2 = new Rect2 (p1,p2);
Point ur2 = a2.upperRight();
Rect2 b2 = new Rect2 (ur2.y, ur2.x, a2.height(), a2.width());
Implementation of the Rect1 class: 
import java.awt.Point;

public class Rect1 {

  // INSTANCE VARIABLES --------------------------------
  private int llx;    // x coordinate of the lower left corner
  private int lly;    // y coordinate of the lower left corner
  private int width;  // width of the rect
  private int height; // height of the rect

  // CONSTRUCTOR METHODS -------------------------------

  // Construct a rect from the lower left (x,y), width, and height.
  public Rect1 (int llx, int lly, int width, int height) {
    this.llx = llx;
    this.lly = lly;
    this.width = width;
    this.height = height;
  }

  // Construct a rect from the lower left and upper right points.
  public Rect1 (Point ll, Point ur) {
    this.llx = ll.x;
    this.lly = ll.y;
    this.width = ur.x - ll.x;
    this.height = ur.y - ll.y;
  }

  // INSTANCE METHODS ----------------------------------

  // Returns the width of this rect. 
  public int width () {
    return width;
  }

  // Returns the height of this rect. 
  public int height () {
    return height;
  }

  // Returns the lower left point of this rect. 
  public Point lowerLeft () {
    return new Point (llx, lly);
  }

  // Returns the upper right point of this rect. 
  public Point upperRight () {
    return new Point (llx + width, lly + height);
  }

}
Implementation of the Rect2 class: 
import java.awt.Point;

public class Rect2 {

  // INSTANCE VARIABLES --------------------------------
  private Point ll;   // lower left corner of rect.
  private Point ur;   // upper right corner of rect.

  // CONSTRUCTOR METHODS -------------------------------

  // Construct a rect from the lower left (x,y), width, and height.
  public Rect2 (int llx, int lly, int width, int height) {
    this.ll = new Point (llx, lly);
    this.ur = new Point (llx + width, lly + height);
  }

  // Construct a rect from the lower left and upper right points.
  public Rect2 (Point ll, Point ur) {
    this.ll = ll;
    this.ur = ur;
  }

  // INSTANCE METHODS ----------------------------------

  // Returns the width of this rect. 
  public int width () {
    return ur.x - ll.x;
  }

  // Returns the height of this rect. 
  public int height () {
    return ur.y - ll.y;
  }

  // Returns the lower left point of this rect. 
  public Point lowerLeft () {
    return ll;
  }

  // Returns the upper right point of this rect. 
  public Point upperRight () {
    return ur;
  }
}

Task 1b

Rect1 and Rect2 illustrate only two of many ways to implement the given Rect contract. In this subtask, you will consider three more implementations.

Below are skeletons of classes Rect3, Rect4, and Rect5, each of which has one constructor method.

Partial Implementation of the Rect3 class: 
public class Rect3 {

  // This declaration allows us to indicate all IntList operations
  // using the prefix "IL."
  private static IntList IL;

  public Rect3 (int llx, int lly, int width, int height) {
    coords = IL.prepend(llx,
              IL.prepend(lly + height, 
               IL.prepend(llx + width,
	        IL.prepend(lly, 
                 IL.empty()))));
  }

}
Partial Implementation of the Rect4 class: 
public class Rect4 {

  public Rect4 (int llx, int lly, int width, int height) {
    area = width * height;
    ul = new Point(llx, lly + height);
    ur = new int [2];
    ur[0] = llx + width;
    ur[1] = lly + height;
  }

}
Partial Implementation of the Rect5 class: 
public class Rect5 {

  public Rect5 (Point ll, Point ur) {
    sumsAndDiffs = new Point [2];
    sumsAndDiffs[0] = new Point(ur.x + ll.x, ur.y + ll.y);
    sumsAndDiffs[1] = new Point(ur.x - ll.x, ur.y - ll.y);
  }

}
For each of the above three class declarations, your goal is to flesh out the rest of the class declaration to correctly implement the Rect contract. To do this, you will need to flesh out the class skeleton with appropriately defined instance variables, the other constructor method, and all instance methods. All of these will need to be consistent with the given constructor method (which you should not change).

Notes:

Task 1c

Draw an object diagram showing the result of executing the following statements: 
Point p1 = new Point (1,2);
Point p2 = new Point (9,6);
Rect3 a3 = new Rect3 (p1,p2);
Point ur3 = a3.upperRight();
Rect3 b3 = new Rect3 (ur3.y, ur3.x, a3.height(), a3.width());
Rect4 a4 = new Rect4 (p1,p2);
Point ur4 = a4.upperRight();
Rect4 b4 = new Rect4 (ur4.y, ur4.x, a4.height(), a4.width());
Rect5 a5 = new Rect5 (p1,p2);
Point ur5 = a5.upperRight();
Rect5 b5 = new Rect5 (ur5.y, ur5.x, a5.height(), a5.width());

Task 2: GubbleWorld

Background

Gubbles are distant relatives of buggles that look like this:

Their heads are filled circles that are 25% of their body length, and their abdomens are filled circles that are 75% of their body length. They also have four legs that project outward from the center of their abdomen. A gubble can be any color.

Like buggles, gubbles live in a two-dimensional world (GubbleWorld) that is similar to BuggleWorld except for the following visual differences:

Below are pictures of some sample GubbleWorld configurations. As is apparent from the top left picture, (1) some instances of GubbleWorld do not have internal walls and (2) it is possible for two or more gubbles to occupy the same grid cell.

Inspired by Stephen Wolfram's book, A New Kind Of Science, gubbles have decided to experiment with cellular automata. One class of cellular automata involves two-dimensional grids whose contents change over time according to local rules that specify the next contents of a subgrid of the cells based on the current contents of that subgrid. A well-known example of this class is John Horton Conway's game of life. (Also see Mitch Resnick & Brian Silverman's active essay, Exploring Emergence.)

Gubbles are investigating their own form of cellular automata in their two-dimensional grid world. They have developed the following set of rules. In all of the rules, the term obstruction refers to either (1) a wall or (2) another gubble. When obstructions are mention as being to the left, front, or right of the gubble, this means the immediate left, immediate front, or immediate right.

  1. If at time t a gubble is alone in a cell and has no obstruction to its front, it goes forward one step. For example:

    Time t Time t+1

  2. If at time t a gubble has obstructions to its front and right but not to its left, then at time t+1 it will turn left and go forward one step. For example, each of the gubbles in the following two pairs of configurations follows this rule:

    Time t Time t+1

  3. If at time t a gubble has obstructions to its left and front but not to its right, then at time t+1 it will turn right and go forward one step. For example, the red gubble in the top pair of configurations below and the red and yellow buggles in the bottom pair below follow this rule. (The magenta and blue gubbles in the bottom pair of configurations are following the "turn to left" rule).

    Time t Time t+1

  4. If at time t a gubble has an obstruction to its front but not to its left or right, then at time t+1 it splits into two gubbles of the same color, one of which turns left and goes forward one step, and the other of which turns right and goes forward one step. For example, all the gubbles below are following this rule.

    Time t Time t+1

  5. If at time t a gubble has obstructions to its left, front, and right, then it dies (sad!) and disappears from the grid at time t+1. For example, the blue gubble below is following this rule. (The yellow gubble is following the "to the left" rule.)

    Time t Time t+1

  6. If at time t two or more gubbles are in the same cell, then they eat each other (gasp!) and disappear by time t+1. For example, all the gubbles below are following this rule:

    Time t Time t+1

It is often the case that several of the above rules will be need to explain how one configuration advances to the next. For example, all rules except for rule 5 are needed to explain how the left configuration transforms to the right configuration below. Make sure you can explain which rule controls the fate of each gubble in the left configuration.

Time t Time t+1

It is worth emphasizing that in configurations with multiple gubbles, the rules are simultaneously applied to all the gubbles in a configuration. In some cases, it is impossible to explain the gubble behavior by applying the rules to the gubbbles sequentially (one by one) in any order. For example, in the following application of rule 4 seen above, the rule must be applied to both the red and blue gubbles simultaneously. If we first applied it to the red gubble, causing it to split in two, then the blue gubble would follow rule 1 and move forward instead of splitting! Similarly, if we first applied rule 4 to the blue gubble, causing it to split in two, then the red gubble would follow rule 1 and move forward instead of splitting.

Time t Time t+1

Below is a an AnimationWorld applet that shows several examples of the above rules in action for some initial configurations of gubbles and walls. You should play with this applet (especially by using the Next button) to make sure that you understand all of the rules that the gubbles are following.

Notes on the above applet:

  • You may have to press the Reset button to refresh the screen before pressing Play or Next.
  • This applet may not run in all browsers. If you have trouble running it, (1) try a different browser or (2) instead download and play with the same applet in ps10_programs/GubbleWorld/Test.
  • You should play with all six initial configurations. You can change the initial configuration by selecting a different name from the leftmost menu. (BTW, the name "Fourmication" is probably not the pun you think it is. Look up the word "formication" in the dictionary!)

Your Task

Your task is to implement the GubbleWorld animation that you played with in the above applet. To do this, you will have to implement (from scratch!) the following three classes:
  1. GubbleWorld: This is a subclass of Sprite that implements an entire GubbleWorld cellular automata as a single sprite. Each call to updateState() on a GubbleWorld instance causes the configuration of the cellular automaton represented by that instance to advance by one time step according the the rules explained above. You must flesh out this class so that it correctly implements the GubbleWorld Contract.
  2. Gubble: This class implements the gubble creatures that live within an instance of GubbleWorld. You must flesh out this class so that it correctly implements the Gubble Contract.
  3. GubbleGroup: This class implements indexed collections of gubbles. Your implementation of GubbleWorld should use instances of GubbleGroup to represent the collection of gubbles that live in a particular configuration. You must flesh out this class so that it correctly implements the GubbleGroup Contract

Notes:

Optional Extra Credit Challenges

GubbleWorld is an excellent starting point for exploring both cellular automata and object-oriented programming in Java. You can earn extra credit points on this assignment by extending your GubbleWorld implementation from Task 2 in various ways. Below are a few suggestions, but you are welcome to design your own extensions. Feel free to talk with Lyn or Elena about any ideas you have.