CS111 Spring 2002 Problem Set 9

CS111, Wellesley College, Spring 2002

Problem Set 9

Due Friday May 3, at 11:59pm

[CS111 Home Page] [Syllabus] [Assignments] [Documentation] [FAQ] [CS Dept.] [CWIS]

About this Problem Set

The purpose of this problem set is to give you experience with declaring Java objects and drawing with Java graphics. In Task 1, you will draw object diagrams showing the state of several objects. In Task 2, you will study data abstraction in the context of simple rectangle objects, In Task 3, you will create a class the models simple cartoon faces, and draw these faces.

There are also two optional extra credit problems. In Extra Credit Challenge 1, you can use Java graphics to draw an interesting picture. Extra Credit Challenge 2 is an open-ended opportunity to use Java graphics to draw any picture(s) of your own design.

All code for this assignment is available in the ps9_programs folder in the cs111 download directory on nike.

How to turn in this Problem Set

You are required to turn in both a hardcopy and a softcopy. For general guidelines on problem set submission, including how to submit a softcopy and how to check if you softcopy submission was successful, click here. Please make sure to keep a copy of your work, either on a zip disk, or in your private directory (or, to play it safe, both).

Hardcopy Submission

Your hardcopy packet should consist of:

The cover page;
Your object diagram from Task 1;
Your object diagram from Task 2a;
The final versions of Rect3.java, Rect4.java, and Rect5.java from Task 2b;
Your object diagram from Task 2c;
The final version of Faces.java from Task 3. If you are unable to complete all the subtasks, turn in the version of your code that solves those subtasks you have completed.

Staple these together, and slide the packet under the door of Elena's office (E127, in minifocus).

Softcopy Submission

You should submit your final version of your ps9_programs folder. In particular,

The Rects subfolder should contain your final versions of Rects3.java, Rects4.java, and Rects5.java,
The Faces subfolder should contain your final version of Faces.java.

Task 1: Tree Node Diagrams

The purpose of this problem is to give you some practice drawing object diagrams. Recall that an object diagram shows a collection of interconnected class instances. Each instance is drawn as a large box that is labelled by the class name and contains the labelled instances variables of the class. Each variable is a small box that contains either a primitive data type (e.g., int, double, boolean, char) or a pointer to another object. These are in the style of Object Land from earlier in the semester.

Consider the following Java class declaration:


class Node {
	
	public int value;
	public Node left;
	public Node right;
	
	public Node (int v, Node l, Node r) {
		this.value = v;
		this.left = l;
		this.right = r;
	}
}

The Node class specifies that instances of the node class have three instance variables: a value variable that holds an integer, and variables left and right that hold pointers to other Node instances. The Node constructor takes an integer and two Node instances and intializes the instance variables with these values.

Here is a sequence of statements that creates and manipulates Node instances:

		Node a = new Node(1,
                  new Node(2, null, null),
                  new Node(3,
                           new Node(4, null, null),
                           null));
a.left.right = a.right.left;
a.left.left = a; 
Node b = a.left; 
b.left.value = a.left.value + b.right.value;

Recall that null denotes the null pointer, a special value that can fill any variable of object type in place of a pointer to an object of that type.

In this problem, you are to draw a single object diagram that depicts the variables and objects created by executing the above five statements. Your diagram should include the local variables a and b as well as all of the Node instances that are created. It should show the state of all variables and objects at the end of the execution of the five statements.

Follow these conventions:

Every variable (both local variables and instance variables) should be drawn as a small box with the name of the variable next to it.
Each instance of the Node class should be draw as a larger box labelled "Node" that contains three instance variables.
A variable that contains the null pointer should have a slash drawn through it.
References should be indicated by drawing pointers rather than using reference labels.
The arrow of a pointer should always point at an instance box. It should never point to a variable box.

Task 2: Data Abstraction with Rects

Rects

A key idea in CS111 is data abstraction -- the notion that "users" can successfully use objects by understanding their contracts without knowing how the contracts have been implemented by the "implementers". Contracts not only serve to simplify the programming task for users, they also give implementers the flexibility to experiment with different ways to implement the same contract.

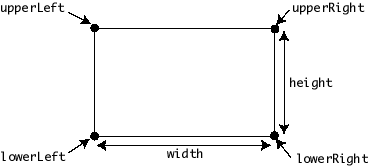
In lecture, we studied the notion of multiple implementations of a data abstraction in the context of a simple rectangle abstraction known as a Rect. Conceptually, an instance of Rect is a rectangle positioned in the standard Cartesian coordinate system:

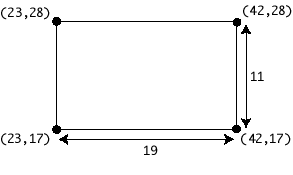
Here is a sample rectangle with lower left point (23,17), width 19, and height 11:

Note that the rectangles we study in this problem are not the same as the java.awt.Rectangle class used in graphics applications, such as Task 3 below.

Below is a simple contract for the Rect class that supports two constructor methods and four instance methods. This class could easily be extended with more methods, such as methods for finding the perimeter or area of a rectangle, or returning its upper left and lower right points. But we've kept the contract small for simplicity's sake.

Rect Contract
Constructor Methods
public Rect (int llx, int lly, int width, int height);
Construct a rect from with lower left point (llx,lly), width width, and height height.
public Rect (Point ll, Point ur);
Construct a rect with lower left point ll and upper right point ur.
Instance Methods
public int width ();
Returns the width of this rect.
public int height ();
Returns the height of this rect.
public Point lowerLeft ();
Returns the lower left point of this rect.
public Point upperRight ();
Returns the upper right point of this rect

As an example, the rectangle depicted above could be created by either of the following constructor method invocations:

new Rect(23, 17, 19, 11);
new Rect(new Point(23, 17), new Point(42, 28));

In the remainder of this problem, you will consider five different implementations of the Rect contract. In order to be able to discuss the different implementations, we will name them Recti, where i ranges between 1 and 5.

Task 2a

Below are the implementations of classes Rect1 and Rect2 that implement the contract for Rect (modulo the change in constructor name). In this subtask, you should draw an object diagram that shows the result of the following sequence of statements:

Point p1 = new Point (1,2);
Point p2 = new Point (9,6);
Rect1 a1 = new Rect1 (p1,p2);
Point ur1 = a1.upperRight();
Rect1 b1 = new Rect1 (ur1.y, ur1.x, a1.height(), a1.width());
Rect2 a2 = new Rect2 (p1,p2);
Point ur2 = a2.upperRight();
Rect2 b2 = new Rect2 (ur2.y, ur2.x, a2.height(), a2.width());

Implementation of the Rect1 class:

import java.awt.Point;

public class Rect1 {

  // INSTANCE VARIABLES --------------------------------
  private int llx;    // x coordinate of the lower left corner
  private int lly;    // y coordinate of the lower left corner
  private int width;  // width of the rect
  private int height; // height of the rect

  // CONSTRUCTOR METHODS -------------------------------

  // Construct a rect from the lower left (x,y), width, and height.
  public Rect1 (int llx, int lly, int width, int height) {
    this.llx = llx;
    this.lly = lly;
    this.width = width;
    this.height = height;
  }

  // Construct a rect from the lower left and upper right points.
  public Rect1 (Point ll, Point ur) {
    this.llx = ll.x;
    this.lly = ll.y;
    this.width = ur.x - ll.x;
    this.height = ur.y - ll.y;
  }

  // INSTANCE METHODS ----------------------------------

  // Returns the width of this rect. 
  public int width () {
    return width;
  }

  // Returns the height of this rect. 
  public int height () {
    return height;
  }

  // Returns the lower left point of this rect. 
  public Point lowerLeft () {
    return new Point (llx, lly);
  }

  // Returns the upper right point of this rect. 
  public Point upperRight () {
    return new Point (llx + width, lly + height);
  }

}

Implementation of the Rect2 class:

import java.awt.Point;

public class Rect2 {

  // INSTANCE VARIABLES --------------------------------
  private Point ll;   // lower left corner of rect.
  private Point ur;   // upper right corner of rect.

  // CONSTRUCTOR METHODS -------------------------------

  // Construct a rect from the lower left (x,y), width, and height.
  public Rect2 (int llx, int lly, int width, int height) {
    this.ll = new Point (llx, lly);
    this.ur = new Point (llx + width, lly + height);
  }

  // Construct a rect from the lower left and upper right points.
  public Rect2 (Point ll, Point ur) {
    this.ll = ll;
    this.ur = ur;
  }

  // INSTANCE METHODS ----------------------------------

  // Returns the width of this rect. 
  public int width () {
    return ur.x - ll.x;
  }

  // Returns the height of this rect. 
  public int height () {
    return ur.y - ll.y;
  }

  // Returns the lower left point of this rect. 
  public Point lowerLeft () {
    return ll;
  }

  // Returns the upper right point of this rect. 
  public Point upperRight () {
    return ur;
  }
}

Task 2b

Rect1 and Rect2 illustrate only two of many ways to implement the given Rect contract. In this subtask, you will consider three more implementations.

Below are skeletons of classes Rect3, Rect4, and Rect5, each of which has one constructor method.

Partial Implementation of the Rect3 class:

public class Rect3 {

  // This declaration allows us to indicate all IntList operations
  // using the prefix "IL."
  private static IntList IL;

  public Rect3 (int llx, int lly, int width, int height) {
    coords = IL.prepend(llx,
              IL.prepend(lly + height, 
               IL.prepend(llx + width,
	        IL.prepend(lly, 
                 IL.empty()))));
  }

}

Partial Implementation of the Rect4 class:

public class Rect4 {

  public Rect4 (int llx, int lly, int width, int height) {
    area = width * height;
    ul = new Point(llx, lly + height);
    ur = new int [2];
    ur[0] = llx + width;
    ur[1] = lly + height;
  }

}

Partial Implementation of the Rect5 class:

public class Rect5 {

  public Rect5 (Point ll, Point ur) {
    sumsAndDiffs = new Point [2];
    sumsAndDiffs[0] = new Point(ur.x + ll.x, ur.y + ll.y);
    sumsAndDiffs[1] = new Point(ur.x - ll.x, ur.y - ll.y);
  }

}

For each of the above three class declarations, your goal is to flesh out the rest of the class declaration to correctly implement the Rect contract. To do this, you will need to flesh out the class skeleton with appropriately defined instance variables, the other constructor method, and all instance methods. All of these will need to be consistent with the given constructor method (which you should not change).

Notes:

The subfolder Rects of ps9_programs contains the implementations of Rect1 and Rect2 as well as the skeletons of Rect3, Rect4, and Rect5. You should flesh out the three skeletons.
When you finish fleshing out a class, you should add the .java file for the class to the Rects.mcp project. You can do this via drag-and-drop (on the Macintosh), or via the Project:Add Files menu item (on both Macs and PCs)
The RectTest class contains code that performs a simple test of the Rect1 and Rect2 implementations. It also contains commented out code that tests the remaining implementations. When you flesh out an implementation, you should uncomment the relevant testing code in RectTest. Compiling and executing the project file Rects.mcp will execute the main() method in the RectTest class and display the results of the tests in the Java Console window.
The Rect3 has been configured with a declaration that allows you to refer to any of the class methods of the IntList by prefixing them with "IL.". For instance: IL.prepend, IL.head, IL.tail, IL.empty, IL.isEmpty.
For Rect5, consider the following. Suppose there are two unknown numbers a and b, and you are given two numbers c and d such that c = a + b and d = a - b. How can you determine the value of a given c and d? How can you determine the value of b given c and d?

Task 2c

Draw an object diagram showing the result of executing the following statements:

Point p1 = new Point (1,2);
Point p2 = new Point (9,6);
Rect3 a3 = new Rect3 (p1,p2);
Point ur3 = a3.upperRight();
Rect3 b3 = new Rect3 (ur3.y, ur3.x, a3.height(), a3.width());
Rect4 a4 = new Rect4 (p1,p2);
Point ur4 = a4.upperRight();
Rect4 b4 = new Rect4 (ur4.y, ur4.x, a4.height(), a4.width());
Rect5 a5 = new Rect5 (p1,p2);
Point ur5 = a5.upperRight();
Rect5 b5 = new Rect5 (ur5.y, ur5.x, a5.height(), a5.width());

Task 3: Faces

In this problem, we will model simple cartoon faces like those shown below:

Each face is characterized by the following state:

Its color.
Its happiness, which is a floating point number that should be between 0.0 (mouth closed) and 1.0 (mouth wide open). A face with happiness value h between 0.0 and 1.0 has its mouth open by a fraction h.
Its sleepiness, which is a floating point number that should be between 0.0 (eyes wide open) and 1.0 (eyes shut). A face with sleepiness value s between 0.0 and 1.0 has its eyelids closed by a fraction s.

For example, the following table shows the values for the color (r = red, g = green, and b = blue), happiness (h) and sleepiness (s) of each face in the corresponding position in the figure above:

r=255, g=0, b=0, h=0.0, s=0.0	r=255, g=63, b=0, h=0.25, s=0.0	r=255, g=127, b=0, h=0.50, s=0.0	r=255, g=191, b=0, h=0.75, s=0.0	r=255, g=255, b=0, h=1.0, s=0.0
r=255, g=0, b=63, h=0.0, s=0.25,	r=255, g=63, b=63, h=0.25, s=0.25	r=255, g=127, b=63, h=0.50, s=0.25	r=255, g=191, b=63, h=0.75, s=0.25	r=255, g=255, b=63, h=1.0, s=0.25
r=255, g=0, b=127, h=0.0, s=0.50	r=255, g=63, b=127, h=0.25, s=0.50	r=255, g=127, b=127, h=0.50, s=0.50	r=255, g=191, b=127, h=0.75, s=0.50	r=255, g=255, b=127, h=1.0, s=0.50
r=255, g=0, b=191, h=0.0, s=0.75	r=255, g=63, b=191, h=0.25, s=0.75	r=255, g=127, b=191, h=0.50, s=0.75	r=255, g=191, b=191, h=0.75, s=0.75	r=255, g=255, b=191, h=1.0, s=0.75
r=255, g=0, b=255, h=0.0, s=1.0,	r=255, g=63, b=255, h=0.25, s=1.0	r=255, g=127, b=255, h=0.50, s=1.0	r=255, g=191, b=255, h=0.75, s=1.0	r=255, g=255, b=255, h=1.0, s=1.0

We will represent a face by an instance of the Face class, which is described by the following contract:

Face Contract

Constructor Methods:
public Face (Color c, double h, double s)
Constructs and returns a Face instance whose color is c, whose happiness is h, and whose sleepiness is s.
public Face ()
Constructs and returns a Face instance whose color is yellow, whose happiness is 1.0, and whose sleepiness is 0.0.
Instance Methods:
public Color getColor()
Returns the color of this face.
public double getHappiness()
Returns the happiness of this face.
public double getSleepiness()
Returns the sleepiness of this face.
public void setColor (Color c)
Changes the color of this face to c.
public void setHappiness (double h)
If h is in the the range [0.0, 1.0], changes the happiness of this face to h. Otherwise, leaves h unchanged and displays an error message indicating h is out of range.
public void setSleepiness (double s)
If s is in the the range [0.0, 1.0], changes the sleepiness of this face to s. Otherwise, leaves s unchanged, and displays an error message indicating s is out of range.
public void draw (Graphics g, Rectangle r)
Draw a picture of this face inscribed in rectangle r within graphics context g. Note that Rectangle is Java's standard rectangle class in the java.awt package, and not any of the rectangle classes described in Task 2 above. See the Rectangle contract page for the Rectangle contract, and the the CS111 Contracts page for other contracts.
public String toString ()
Return a string representation of this face. A face with red/green/blue color values r, g, and b and with happiness h and sleepiness s should have the following string representation:

"Face[color=java.awt.Color[r=r,g=g,b=b]; happiness=h; sleepiness=s]"
Note that you can use the toString() method for colors to get the string representation of a color.

Task 3a: The Face Class

In this subtask, you will define a preliminary version of the Face class. A skeleton of this class can be found in the file Face.java within the Faces subfolder of the ps9 folder. You are flesh out the skelelton with instance variable declarations, constructor method declarations, and instance method declarations so that it implements the Face contract given above except for the draw() method. Rather than actually drawing the face in the given rectangle, your initial draw() method should simply display a string representation of the face in the Java Console window (via System.out.println).

For example, when you test the default applet ManyFaces.html, you should get the following output:

Face[color=java.awt.Color[r=255,g=0,b=0]; happiness=0.0; sleepiness=0.0]
Face[color=java.awt.Color[r=255,g=0,b=63]; happiness=0.0; sleepiness=0.25]
Face[color=java.awt.Color[r=255,g=0,b=127]; happiness=0.0; sleepiness=0.5]
Face[color=java.awt.Color[r=255,g=0,b=191]; happiness=0.0; sleepiness=0.75]
Face[color=java.awt.Color[r=255,g=0,b=255]; happiness=0.0; sleepiness=1.0]
Face[color=java.awt.Color[r=255,g=63,b=0]; happiness=0.25; sleepiness=0.0]
Face[color=java.awt.Color[r=255,g=63,b=63]; happiness=0.25; sleepiness=0.25]
Face[color=java.awt.Color[r=255,g=63,b=127]; happiness=0.25; sleepiness=0.5]
Face[color=java.awt.Color[r=255,g=63,b=191]; happiness=0.25; sleepiness=0.75]
Face[color=java.awt.Color[r=255,g=63,b=255]; happiness=0.25; sleepiness=1.0]
Face[color=java.awt.Color[r=255,g=127,b=0]; happiness=0.5; sleepiness=0.0]
Face[color=java.awt.Color[r=255,g=127,b=63]; happiness=0.5; sleepiness=0.25]
Face[color=java.awt.Color[r=255,g=127,b=127]; happiness=0.5; sleepiness=0.5]
Face[color=java.awt.Color[r=255,g=127,b=191]; happiness=0.5; sleepiness=0.75]
Face[color=java.awt.Color[r=255,g=127,b=255]; happiness=0.5; sleepiness=1.0]
Face[color=java.awt.Color[r=255,g=191,b=0]; happiness=0.75; sleepiness=0.0]
Face[color=java.awt.Color[r=255,g=191,b=63]; happiness=0.75; sleepiness=0.25]
Face[color=java.awt.Color[r=255,g=191,b=127]; happiness=0.75; sleepiness=0.5]
Face[color=java.awt.Color[r=255,g=191,b=191]; happiness=0.75; sleepiness=0.75]
Face[color=java.awt.Color[r=255,g=191,b=255]; happiness=0.75; sleepiness=1.0]
Face[color=java.awt.Color[r=255,g=255,b=0]; happiness=1.0; sleepiness=0.0]
Face[color=java.awt.Color[r=255,g=255,b=63]; happiness=1.0; sleepiness=0.25]
Face[color=java.awt.Color[r=255,g=255,b=127]; happiness=1.0; sleepiness=0.5]
Face[color=java.awt.Color[r=255,g=255,b=191]; happiness=1.0; sleepiness=0.75]
Face[color=java.awt.Color[r=255,g=255,b=255]; happiness=1.0; sleepiness=1.0]

Task 3b: Put on a Happy Face

In this part, you are to change the implementation of your draw() method so that it draws an alert, happy face with the face's color in the specified rectangle. Your method should ignore the actual happiness of the face and simply assume that it is 1.0. Similarly, your method should ignore the actual sleepiness of the face, and just assume that it is 0.0. However, your method should draw the face using the actual color of the face. So when you run the ManyFaces.html applet, the goal is to get the following picture:

Below is a diagram of a happy face inscribed in the unit square indicating the placement of the eyes, nose, and mouth. You should draw the happy face exactly as depicted in this diagram.

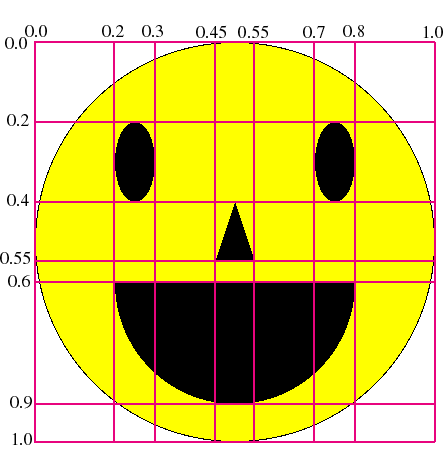
Notes:

In order to draw the face, you will need to use various drawing methods of the Graphics class presented in lecture and lab. As part of doing this problem, you should consult the contract for the Graphics class. You will also need to use the contracts for the Rectangle and Polygon classes.
For examples of each of the kinds of shapes out of which a face is compose, study the code in the following file from Lyn's lecture: /cs111/download/lec22_graphics_lyn/GraphicsDemo.java.
The drawing methods in the Graphics class expect integers as arguments. The java compiler will complain if you pass a floating point number rather than an integer as an argument to one of these methods. For instance, if g denotes a Graphics instance and r denotes a Rectangle instance, then the following is incorrect:
```
g.drawLine(r.x + (0.1 * r.width), 
           r.y + (0.3 * r.height),
           r.x + (0.7 * r.width),
           r.y + (0.6 * r.height));
```
This problem can be fixed by using an integer cast expression (int) E to convert the result of a floating point expression E to an integer. A corrected version of the above example is:
```
g.drawLine(r.x + (int) (0.1 * r.width), 
           r.y + (int) (0.3 * r.height),  
           r.x + (int) (0.7 * r.width),
           r.y + (int) (0.6 * r.height));
```
You can view a large version of a happy face by running the OneFace.html applet. You can do this by moving OneFace.html before ManyFaces.html in the LinkOrder tab of the Face.mcp project file. Here is the window produce by this applet:

Task 3c: Sleepy Faces

In this part, you are to modify the implementation of your draw() method so that it correctly shows droopy eyelids for sleepy faces, as shown below:

A face with sleepiness factor s (between 0.0 and 1.0) should have "eyelids" covering a fraction s of the height of the eyes from the top to the bottom. This effect can be achieved as follows:

Draw the normal "alert" eyes as filled black ovals.
Draw a filled rectangle with the color of the face that covers the appropriate fraction of the eyes.
Draw unfilled black ovals around the eyes.

Note that, according to its contract, the drawOval() method covers an area that is width + 1 pixels wide and height + 1 pixels tall. In contrast, the the fillOval() method covers an area that is width pixels wide and height pixels tall. Because of this discrepency, to get your picture to "look right" you may need to subtract 1 from the width and height arguments of drawOval().

Task 3d: Drawing Happiness

In this part, your goal is to modify the mouth-drawing part of your drawMethod() so that it takes into account the happiness of the face. A face with happiness 0.0 should have a line as a mouth, while larger happiness values (up to 1.0) should be drawn as filled half-ovals whose height is proportional to the happiness value.

For example, here are faces whose happiness value changes from left to right:

Here is the specification for the mouth that you should implement:

The mouth should have a width that is 0.6 times the width of the face.
The mouth should be horizontally centered in the face.
The height of the mouth should be the happiness value times 0.3 times the height of the face, but should never be smaller than 1. The "never smaller than" effect can be achieved using the Math.max() method, which returns the maximum of two integers.
The mouth should be vertically centered about a horizontal line that is 0.75 the way down the face.

The above specification can be implemented via a single invocation of the fillArc() method that handles all happiness values between 0.0 and 1.0. The key to getting this to work is to determine the coordinates of the rectangle in which the arc is inscribed as a function of the happiness value. Do not attempt to do this by trial and error! Instead, determine the correct formula on a sheet of paper before you attempt to implement this part!

Extra Credit Challenge 1: Rainy Day

This is a completely optional problem. You should only attempt it after completing the rest of the assignment.

In this challenge, you are to create from scratch an applet that draws the following picture (due to Elena):

This picture is taken from CS111 Fall 2001 Lab 12. For more details, consult the web page for this lab.

Extra Credit Challenge 2: Create Your Own Picture

This is a completely optional problem. You should only attempt it after completing the rest of the assignment.

You can use Java graphics as a tool to create fascinating pictures. Here is a chance to be artistically creative and earn some extra credit points at the same time.

For this challenge, flesh out the paint() method in the MyPicture class within the MyPicture folder to draw whatever picture you imagine. If you like, you can draw more than one by making copies of MyPicture.java where the files (and the contained class) have different names.

Notes:

This is the only problem on this problem set in which you may collaborate with others in the class. Feel free to collaborate with as many people as you want.
There will be no prizes for designs in this challenge. But all extra credit assignments submitted will be posted on an "exhibition page" so that you can share your designs with the class.
If you need help to do something fancy, please talk to the instructors and/or TAs.
Extra credit will be given on this problem in proportion to the creativity and artistry in your designs, as well as the level of technical challenge.