CS111 Lab 3 Solutions -- colors

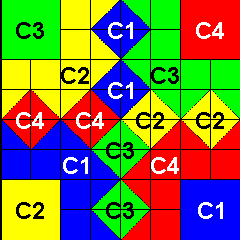
Problem:

colors Solution

Taking a look at the picture, we try to look for patterns. In particular, it is useful to be on the lookout for the following patterns which are available to us through our contract.

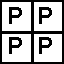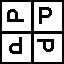patch(Color)	triangles(Color1, Color2)	fourPics(P1,P2,P3,P4)	fourSame(P)	rotations(P)	corner(P1,P2)

Dividing the problem -- colors

Looking at the colors, we see that we can divide it into four quarters like so:

=

We notice that the four quarters look like the same pattern but the pattern is rotated clockwise 90 degrees as we go from quadrant to quadrant in a clockwise manner. Let's call the basic pattern (in the top right corner) a colorsQuarter. We pick that pattern to be the basic pattern so that we can use the rotations method that is given to us. The entire colors pattern can now be described by the following bit of pseudocode
pseudocode: colors = rotations(colorsQuarter)
But wait! That won't quite work because the four quarters are not exactly the same. The pattern is the same, but the colors are different. So, we can't use the rotations method which will only take one pattern and rotate it around for us. Instead, we'll have to rotate the patterns ourself. Here's our revised pseudocode
pseudocode: colors = fourPics(clockwise270(colorsQuarter(3 colors)), colorsQuarter(another 3 colors),
  clockwise180(colorsQuarter(yet another 3 colors)), clockwise90(colorsQuarter(some other 3 colors)))
We have now divided the big problem colors into solving a smaller subproblem colorsQuarter. The pseudocode above tells us how to glue the subproblem solution together to form the solution to the original problem.

Dividing the problem -- colorsQuarter

Now we need to figure out how to create a colorsQuarter. Since it's not entirely obvious, we again apply the Divide, Conquer, and Glue strategy. Taking a look at the colorsQuarter, we notice that we can also divide that into four quarters like so:

=

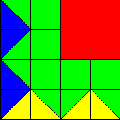We see that we have a red patch in the top right quadrant and two distinct color patterns. Let's call them colorsPattern1 and colorsPattern2 like so:

colorsPattern1

colorsPattern2

We notice that the top left quadrant and the bottom right quadrant are both instances of colorsPattern1. Their relationship can be expressed as follows:

Take this and rotate it 90 degrees clockwise to get

We'll have to keep in mind that although the pattern is the same, the colors used in the two quadrants are different. Now we can write the following bit of pseudocode
pseudocode: colorsQuarter = fourPics(clockwise90(colorsPattern1(2 colors)), redPatch,
  colorsPattern2(3 colors), colorsPattern1(another 2 colors))
We have now divided the big problem colorsQuarter into one basic building block redPatch and two smaller subproblems colorsPattern1 and colorsPattern2. The pseudocode above tells us how to glue the subproblem solutions together to form the solution to the original problem.

Dividing the problem -- colorsPattern1

Now we need to figure out how to create a colorsPattern1. We can again divide this pattern into quadrants like so:

=

Now everything is a basic building block. We have two green patches in the upper quadrants and two yellow green triangles in the bottom quadrants. The relationship between the two yellow green triangles can be expressed in multiple ways as follows:

Take this and	flip it vertically	to get
	rotate it 270 degrees clockwise

You could also create the bottom left corner by starting with a green yellow triangle instead like so:

Take this and rotate it 90 degrees clockwise to get

Now we can write the following bit of pseudocode
pseudocode: colorsPattern1 = fourPics(greenPatch, greenPatch, flipVertically(yellowGreenTriangles), yellowGreenTriangles)
We have now divided the big problem colorsPattern1 into basic building blocks so now we can conquer this problem!

Conquering the problem -- colorsPattern1

Now we need to write the actual code to create the colorsPattern1. We should write the code so that we can generate this pattern in any two colors. To do this, let's first decide how to label our colors. Why don't we do the following:

c1 will be the color that fills the bottom triangles
c2 will be the other color which fills most of the pattern

Here's our code for the colorsPattern1 method which will return the colorsPattern1 Picture:

public Picture colorsPattern1 (Color c1, Color c2) {
  Picture c1c2Triangles = triangles(c1, c2);   // create triangles of Colors c1 and c2
  Picture c2Patch = patch(c2);   // create a patch of Color c2
  return fourPics(c2Patch, c2Patch, flipVertically(c1c2Triangles), c1c2Triangles);
}

Dividing the problem -- colorsPattern2

Now we need to figure out how to create a colorsPattern2. We can again divide this pattern into quadrants like so:

=

Now everything is a basic building block. We have a green patch in the top right quadrant and three different colored triangles in the other quadrants. The top left quadrant has a blue green triangle. The bottom right quadrant has a yellow green triangle. We can create the bottom left quadrant out of blue yellow or yellow blue triangles like so:

Take this and rotate it 90 degrees clockwise to get

Take this and rotate it 270 degrees clockwise to get

Now we can write the following bit of pseudocode
pseudocode: colorsPattern2 = fourPics(blueGreenTriangles, greenPatch,
  clockwise90(blueYellowTriangles), yellowGreenTriangles)
We have now divided the big problem colorsPattern2 into basic building blocks so now we can conquer this problem!

Conquering the problem -- colorsPattern2

Now we need to write the actual code to create the colorsPattern2. We should write the code so that we can generate this pattern in any three colors. To do this, let's first decide how to label our colors. Why don't we do the following:

c1 will be the color that fills the triangles on the left
c2 will be the color that fills the triangles on the bottom
c3 will be the color that fills the rest of the pattern

Here's our code for the colorsPattern2 method which will return the colorsPattern2 Picture:

public Picture colorsPattern2 (Color c1, Color c2, Color c3) {
  Picture c1c3Triangles = triangles(c1, c3);  // for top left quadrant
  Picture c3Patch = patch(c3);                // for top right quadrant
  Picture c1c2Triangles = triangles(c1, c2);  // for bottom left quadrant
  Picture c2c3Triangles = triangles(c2, c3);  // for bottom right quadrant
  return fourPics(c1c3Triangles, c3Patch, clockwise90(c1c2Triangles), c2c3Triangles);
}

Conquering the problem -- colorsQuarter

Now that we have solutions for colorsPattern1 and colorsPattern2, we can write up our solution for colorsQuarter.
First, though, we need to decide how to label our colors. Let's agree on the following:

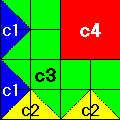
c1 will be the color that fills the triangles on the left
c2 will be the color that fills the triangles on the bottom
c3 will be the color that fills the center of the pattern
c4 will be the color that fills the top right quadrant

Here's our code for colorsQuarter

public Picture colorsQuarter (Color c1, Color c2, Color c3, Color c4) {
  Picture pattern1Top = colorsPattern1(c1, c3);    // for top left quadrant
  Picture c4Patch = patch(c4);                     // for top right quadrant
  Picture pattern2 = colorsPattern2(c1, c2, c3);   // for bottom left quadrant
  Picture pattern1Bottom = colorsPattern1(c2, c3); // for bottom right quadrant
  return fourPics(clockwise90(pattern1Top), c4Patch,
                  pattern2, pattern1Bottom);
}

Conquering the problem -- colors

Now that we have a solution for colorsQuarter, we can write up our solution for colors.
First, though, we need to label our colors. Let's do it like so:

public Picture colors (Color c1, Color c2, Color c3, Color c4) {
  return fourPics(clockwise270(colorsQuarter(c4,c1,c2,c3)), // top left
                  colorsQuarter(c1,c2,c3,c4),               // top right
                  clockwise180(colorsQuarter(c3,c4,c1,c2)), // bottom left
                  clockwise90(colorsQuarter(c2,c3,c4,c1))); // bottom right
}

Using our solutions

To actually see our solutions we need to add picture choices to our applet. Add the following code to the initializePictureChoices method to see the solution to the main problem and all the subproblems that we solved.

// see the colors
addPictureChoice("colors", colors(Color.blue, Color.yellow, Color.green, Color.red));

// see the colorsQuarter
addPictureChoice("colorsQuarter", colorsQuarter(Color.blue, Color.yellow, Color.green, Color.red));

// see the colorsPattern1
addPictureChoice("colorsPattern1", colorsPattern1(Color.yellow, Color.green));

// see the colorsPattern2
addPictureChoice("colorsPattern2", colorsPattern2(Color.blue, Color.yellow, Color.green));