CS111 Lab 3 Solutions -- checkerboard

Problem:

checkerboard Solution

Taking a look at the picture, we try to look for patterns. In particular, it is useful to be on the lookout for the following patterns which are available to us through our contract.

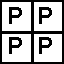patch(Color)	triangles(Color1, Color2)	fourPics(P1,P2,P3,P4)	fourSame(P)	rotations(P)	corner(P1,P2)

Dividing the problem -- checkerboard

Looking at the checkerboard, we see that we can divide it into four quarters which are all the same, like so:

=

If we call each quarter a checkerboardQuarter, we can write the following bit of pseudocode
pseudocode: checkerboard = fourSame(checkerboardQuarter)
We have now divided the big problem checkerboard into solving a smaller subproblem checkerboardQuarter. The pseudocode above tells us how to glue the subproblem solution together to form the solution to the original problem.

Dividing the problem -- checkerboardQuarter

Now we need to figure out how to create a checkerboardQuarter. Since it's not entirely obvious, we again apply the Divide, Conquer, and Glue strategy. Taking a look at the checkerboardQuarter, we notice that we can also divide that into four quarters which are all the same like so:

=

If we call each quarter a checkerboardUnit, we can write the following bit of pseudocode
pseudocode: checkerboardQuarter = fourSame(checkerboardUnit)
We have now divided the big problem checkerboardQuarter into solving a smaller subproblem checkerboardUnit. The pseudocode above tells us how to glue the subproblem solution together to form the solution to the original problem.

Dividing the problem -- checkerboardUnit

Now we need to figure out how to create a checkerboardUnit. We see that we have two black patches and two red patches arranged in a 2 by 2 grid like so:

=

We can write the following bit of pseudocode
pseudocode: checkerboardUnit = fourPics(redPatch, blackPatch, blackPatch, redPatch)
We have now divided the big problem checkerboardUnit into basic building blocks so now we can conquer this problem!

Conquering the problem -- checkerboardUnit

Now we need to write the actual code to create the checkerboardUnit. We should write the code so that we can generate checkerboards of any two colors. To do this, let's first decide how to label our colors. Why don't we do the following:

c1 will be the color at the bottom left corner
c2 will be the other color

Here's our code for the checkerboardUnit method which will return the checkerboardUnit Picture:

public Picture checkerboardUnit (Color c1, Color c2) {
  Picture c1Patch = patch(c1);   // create the patch of Color c1
  Picture c2Patch = patch(c2);   // create the patch of Color c2
  return fourPics(c2Patch, c1Patch, c1Patch, c2Patch);
}

Conquering the problem -- checkerboardQuarter

Now that we have a solution for checkerboardUnit, we can write up our solution for checkerboardQuarter. Here it is

public Picture checkerboardQuarter (Color c1, Color c2) {
  return fourSame(checkerboardUnit(c1,c2));
}

Conquering the problem -- checkerboard

Now that we have a solution for checkerboardQuarter, we can write up our solution for checkerboard. Here it is

public Picture checkerboard (Color c1, Color c2) {
  return fourSame(checkerboardQuarter(c1,c2));
}

Using our solutions

To actually see our solutions we need to add picture choices to our applet. Add the following code to the initializePictureChoices method to see the solution to the main problem and all the subproblems that we solved.

// see the checkerboard
addPictureChoice("checkerboard", checkerboard(Color.black, Color.red));

// see the checkerboardQuarter
addPictureChoice("checkerboardQuarter", checkerboardQuarter(Color.black, Color.red));

// see the checkerboardUnit
addPictureChoice("checkerboardUnit", checkerboardUnit(Color.black, Color.red));