CS111 Fall '99 Problem Set 8

CS111, Wellesley College, Fall 1999

Problem Set 8

Due: Tuesday, November 23 by 4:00 p.m.

[CS111 Home Page] [Syllabus] [Lecture Notes] [Assignments] [Programs] [Documentation] [Software Installation] [FAQ] [CS Dept.] [CWIS]

This is the corrected version of problem set 8. The definitions of `isBst`, `isInTree`, and `pathList` have been changed and the base case for `delete` has been changed.

Reading Assignment:

The reading assignment for this problem set is all on one web page and covers four topics which will be used in the problem set.

IntList Contract and Examples
IntListList Contract and Examples
IntTree Contract and Examples
Box-and-Pointer conventions for binary trees

Optional reading: Notes on permutations and iteration in PictureWorld.

About this Problem Set

The purpose of this problem set is to give you experience with three topics: lists of lists, binary trees, and iteration. For the list of lists problem we will be working with the IntListList data structure which is described in the reading for this problem set. There are three problems in this problem set. Problems 2 and 3 have multiple tasks.

How to turn in this Problem Set

Softcopy submission: Save the modified ChangeMaker.java, BST.java and NestedFrames.java files in the ps8_programs folder. Upload the entire folder (including all the other .java and .class files -- everything) to your ps8 drop folder.

Hardcopy submission: Turn in only one package of hardcopy materials. Staple your files together and submit your hardcopy package by placing it in the box outside of Lyn's office (121B, behind the mini-focus consultant's desk). Your package should include printouts of

cover page on top
ChangeMaker.java from Homework Problem 1
Tree diagram and BST.java from Homework Problem 2
NestedFrames.java from Homework Problem 3

Reminders

Be sure to double check that your folder and files were actually uploaded.
Keep a personal back-up of every file that you upload.
If you have trouble uploading files, it may be because you have reached the limits of your Nike file system quota. In this case, you need to delete some of your old files, either from your home directory or your drop folders (which are also counted toward your quota). To delete a file in Fetch, just drag it to the Trash.

Homework Problem 1: Making Change

Lists of lists are useful data structures for holding lists of possibilities. We can use them to hold the list of all permutations of a set of numbers like we saw done in lab. The problem here will be to use lists of lists to represent all the possible ways of making change for a given amount of money given an unlimited amount of certain denominations. Some examples are given below (assume all values are in cents).

Amount to change Denominations Ways to Make Change
5 [5,1]
[[5], [1,1,1,1,1] ]
1 nickel or 5 pennies

16 [10,5,1]
[[10, 5, 1], [10, 1, 1, 1, 1, 1, 1], [5, 5, 5, 1], [5, 5, 1, 1, 1, 1, 1, 1], [5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] ]

Amount to change	Denominations	Ways to Make Change
5	[5,1]	[[5], [1,1,1,1,1] ] 1 nickel or 5 pennies
16	[10,5,1]	[[10, 5, 1], [10, 1, 1, 1, 1, 1, 1], [5, 5, 5, 1], [5, 5, 1, 1, 1, 1, 1, 1], [5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] ]

Your goal is to formulate a strategy that will list all the possible ways to make change for a given amount of money with a list of possible denominations provided in descending order of value. You will be completing the method makeChange of the ChangeMaker class. The skeleton for the method is provided below:

public static IntListList makeChange (int amount, IntList coins)
Returns a list of possible ways to make change for the amount specified with the coins available. Assume coins are given in descending order of value.

Notes

Modify the ChangeMaker.java file. Test your solutions by running ChangeMakerTest.html. The correct output for the test cases is provided at the end of this problem description. You need to get the same number of ways to make change and the same ways to make change as listed, but you may list the ways to make change in any order and may list the coins in any order.

Since makeChange involves working with IntList and IntListList lists, we can no longer just use list methods and operators without the class name because Java won't know which method we want (i.e. do we want the one that applies to the IntList or the IntListList class?). Instead, we must specify the name of the class with the method (e.g. IntList.prepend or IntListList.prepend). However, specifying the full name of the class makes the code harder to read so we have provided you with the following "shortcut" way to refer to IntList and IntListList methods and operators for doing this problem.

IntList Methods (IL)	IntList Operators (ILO)	IntListList Methods (ILL)	IntListList Operators (ILLO)
IL.empty IL.prepend IL.head IL.tail IL.isEmpty	ILO.length ILO.append ILO.postpend	ILL.empty ILL.prepend ILL.head ILL.tail ILL.isEmpty	ILLO.length ILLO.append ILLO.postpend

Correct Test Case Answers


----------------------------------------------------
There are 2 ways to make change for 5 cents using [10, 5, 1]:
[[5],
 [1, 1, 1, 1, 1]
 ]
----------------------------------------------------
There are 6 ways to make change for 16 cents using [10, 5, 1]:
[[10, 5, 1],
 [10, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 1],
 [5, 5, 1, 1, 1, 1, 1, 1],
 [5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
 ]
----------------------------------------------------
There are 13 ways to make change for 26 cents using [25, 10, 5, 1]:
[[25, 1],
 [10, 10, 5, 1],
 [10, 10, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 5, 1],
 [10, 5, 5, 1, 1, 1, 1, 1, 1],
 [10, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 5, 1],
 [5, 5, 5, 5, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
 ]
----------------------------------------------------
There are 60 ways to make change for 56 cents using [25, 10, 5, 1]:
[[25, 25, 5, 1],
 [25, 25, 1, 1, 1, 1, 1, 1],
 [25, 10, 10, 10, 1],
 [25, 10, 10, 5, 5, 1],
 [25, 10, 10, 5, 1, 1, 1, 1, 1, 1],
 [25, 10, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 10, 5, 5, 5, 5, 1],
 [25, 10, 5, 5, 5, 1, 1, 1, 1, 1, 1],
 [25, 10, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 10, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 5, 5, 5, 5, 5, 5, 1],
 [25, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1],
 [25, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [25, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 10, 10, 5, 1],
 [10, 10, 10, 10, 10, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 10, 5, 5, 5, 1],
 [10, 10, 10, 10, 5, 5, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 10, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 5, 5, 5, 5, 5, 1],
 [10, 10, 10, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 5, 5, 5, 5, 5, 5, 5, 1],
 [10, 10, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1],
 [10, 10, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 5, 5, 5, 5, 5, 5, 5, 1],
 [10, 5, 5, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [10, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 1],
 [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
 ]
----------------------------------------------------
There are 2 ways to make change for 15 cents using [10, 5]:
[[10, 5],
 [5, 5, 5]
 ]
----------------------------------------------------
There are 0 ways to make change for 16 cents using [10, 5]:
[ ]
----------------------------------------------------

Homework Problem 2: Binary Search Trees

A binary search tree (BST) is a tree which encode the binary search strategy. A BST has the property that each tree node contains a value which is greater than or equal to all the values in its left subtree and less than or equal to all the values in its right subtree. For a given set of numbers, there are multiple ways to arrange them into a binary tree that meets the binary search tree property. For example, given the set of numbers (1,2,3,4,5) we can arrange them into binary trees as shown below:

not a binary search tree binary search tree 1 binary search tree 2

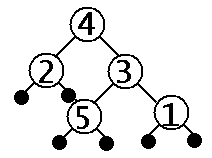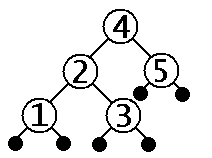We can implement a binary search tree involving integers in Java by extending the IntTree class. A binary search tree is a kind of IntTree with additional properties. To do this, we will create a new class called BST and inside the class we will place useful methods for working with binary search trees.

public class BST extends IntTree {
  // place useful binary search tree methods here
}

The following methods have been defined for you already. These are all methods that you should be able to write yourself.

	
public static int min (IntTree bst) {
  // Returns the minimum value in an integer binary search tree;
  // returns the maximum integer value if given a leaf.
  if (isLeaf(bst)) {
    return Integer.MAX_VALUE;
  } else if (isLeaf(left(bst))) {
    return value(bst);
  } else {
    return min(left(bst));
  }
}
	
public static int max (IntTree bst) {
  // Returns the maximum value in an integer binary search tree;
  // returns the minimum integer value if given a leaf.
  if (isLeaf(bst)) {
    return Integer.MIN_VALUE;
  } else if (isLeaf(right(bst))) {
    return value(bst);
  } else {
    return max(right(bst));
  }
}

public static boolean isBST (IntTree t) {
  // Returns true if t is an integer binary search tree; otherwise, returns false.
  if (isLeaf(t)) {
    return true;
  } else {
    return (value(t)>=max(left(t))) &&
           (value(t)<=min(right(t))) &&
           isBST(left(t)) && isBST(right(t));
  }
}

public static boolean isInTree (int n, IntTree bst) {
  // Returns true is n is in the binary search tree; otherwise, returns false.
  if (isLeaf(bst)) {
    return false;
  } else if (n==value(bst)) {
    return true;
  } else if (n < value(bst)) {
    return isInTree(n, left(bst));
  } else { // (n > value(bst))
    return isInTree(n, right(bst));
  }
}

public static IntList pathList (int v, IntTree bst) {
  // Returns a list of the values one must pass through while searching for the value v in the tree.
  if (isLeaf(bst)) {
    return IL.empty();
  } else if (v == value(bst)) {
    return IL.prepend(v, IL.empty());
  } else if (v < value(bst)) {
    return IL.prepend(value(bst), pathList(v,left(bst)));
  } else { // v > value(bst) 
    return IL.prepend(value(bst), pathList(v,right(bst)));
  }
}

This problem involves three tasks described below:

Task 1: Drawing box-and-pointer diagram for `insert`

Let's say we have a binary search tree. What if we want to add another element to the binary search tree? How can we do so? One possible implementation of insert is provided below:

public static IntTree insert (int x, IntTree bst) {
  // Returns the result of inserting x in bst. 
  if (isLeaf(bst)) {
    return node(x, leaf(), leaf());
  } else if (x>value(bst)) {
    return node(value(bst),
                left(bst),
                insert(x,right(bst)));
  } else { // x<=value(bst)
    return node(value(bst),
                insert(x,left(bst)),
                right(bst));
  }
}

Task 1a: Explain clearly, but succinctly, in words (English) how the stategy for inserting an integer into a binary tree works.

Task 1b: Draw the box-and-pointer diagram for the following sequence of actions:

IntTree t1 = node(10,
                  node(5
                       node(3,leaf(),leaf()),
                       node(8,leaf(),leaf())),
                  node(12,
                       leaf(),
                       node(17,
                            node(13,leaf(),leaf()),
                            leaf())));
IntTree t2 = insert(4, t1);
IntTree t3 = insert(9, t1);
IntTree t4 = insert(13, t1);

Task 2: Implementing `delete`

Being able to delete elements from a binary search tree is also useful. One strategy for accomplishing deletion of an element x from a binary tree is outlined below:

if the tree is a leaf, return the tree
if x is greater than the value of the tree, delete x from the right subtree
if x is less than the value of the tree, delete x from the left subtree
otherwise, x must be the value of the tree; in this case,
- if x has no children, return a leaf
- if x has one child, return the non-leaf subtree
- otherwise, return a tree node with the next largest value after x (the successor value) and with the same left subtree and with the same right subtree but with the successor removed

We have provided you with a skeleton for the delete method. Your task is to fill it in so that it implements the strategy for deletion outlined above.

public static IntTree delete (int x, IntTree bst)
  // Returns the result of deleting one instance of x in bst.

Task 3: Implementing `inOrderList`

In lecture we covered how to print out the elements of a tree traversal in preOrder, inOrder, and postOrder order. It's a little different to convert a tree to a list. A binary search tree has the nice property that if you print out its elements in inOrder order, then the elements will be sorted from the smallest to the largest value. We'd like to have a method inOrderList which takes a tree (any tree) and gives us back a list of the elements of the tree in inOrder order. We have provided you with a skeleton for the inOrderList method. Your task is to fill it in so that it prints out the elements of a given tree in inOrder order.

public static IntList inOrderList (IntTree t)
  // Returns a list containing the elements of t in in-order.

Notes

Modify the BST.java file. Test your solutions by running BSTTest.html. The correct output for the test cases is provided at the end of this problem description.
For inOrderList you will need to use the same abbreviations as in problem 1 of this homework in order to use IntList methods and operators.
The IntTree methods derived in lecture are available in the file IntTreeOps.java which is included with the problem set code. You should understsnd all the methods defined in that file.

Correct Test Case Answers


--------------------------------------------------------
Sample binary search trees:
t0 = *
t1 = (* 10 *)
t2 = ((* 10 *) 20 *)
t3 = ((* 10 *) 20 (* 30 *))
t4 = ((* 10 (* 20 *)) 30 (* 40 *))
t5 = (* 10 (* 20 (* 30 (* 40 (* 50 *)))))
t6 = (((* 10 *) 20 (* 30 *)) 40 ((* 50 *) 60 *))
t7 = (((* 10 *) 20 (* 30 (* 40 *))) 50 (* 60 *))
t8 = ((* 10 ((* 20 *) 30 *)) 40 ((* 50 *) 60 (* 70 (* 80 (* 90 *)))))
--------------------------------------------------------
delete(10, t0) = *
delete(10, t1) = *
delete(10, t2) = (* 20 *)
delete(10, t3) = (* 20 (* 30 *))
delete(10, t4) = ((* 20 *) 30 (* 40 *))
delete(10, t5) = (* 20 (* 30 (* 40 (* 50 *))))
delete(10, t6) = ((* 20 (* 30 *)) 40 ((* 50 *) 60 *))
delete(10, t7) = ((* 20 (* 30 (* 40 *))) 50 (* 60 *))
delete(10, t8) = (((* 20 *) 30 *) 40 ((* 50 *) 60 (* 70 (* 80 (* 90 *)))))
--------------------------------------------------------
delete(20, t0) = *
delete(20, t1) = (* 10 *)
delete(20, t2) = (* 10 *)
delete(20, t3) = ((* 10 *) 30 *)
delete(20, t4) = ((* 10 *) 30 (* 40 *))
delete(20, t5) = (* 10 (* 30 (* 40 (* 50 *))))
delete(20, t6) = (((* 10 *) 30 *) 40 ((* 50 *) 60 *))
delete(20, t7) = (((* 10 *) 30 (* 40 *)) 50 (* 60 *))
delete(20, t8) = ((* 10 (* 30 *)) 40 ((* 50 *) 60 (* 70 (* 80 (* 90 *)))))
--------------------------------------------------------
delete(50, t0) = *
delete(50, t1) = (* 10 *)
delete(50, t2) = ((* 10 *) 20 *)
delete(50, t3) = ((* 10 *) 20 (* 30 *))
delete(50, t4) = ((* 10 (* 20 *)) 30 (* 40 *))
delete(50, t5) = (* 10 (* 20 (* 30 (* 40 *))))
delete(50, t6) = (((* 10 *) 20 (* 30 *)) 40 (* 60 *))
delete(50, t7) = (((* 10 *) 20 (* 30 (* 40 *))) 60 *)
delete(50, t8) = ((* 10 ((* 20 *) 30 *)) 40 (* 60 (* 70 (* 80 (* 90 *)))))
--------------------------------------------------------
inOrderList(t0) = [ ]
inOrderList(t1) = [10]
inOrderList(t2) = [10, 20]
inOrderList(t3) = [10, 20, 30]
inOrderList(t4) = [10, 20, 30, 40]
inOrderList(t5) = [10, 20, 30, 40, 50]
inOrderList(t6) = [10, 20, 30, 40, 50, 60]
inOrderList(t7) = [10, 20, 30, 40, 50, 60]
inOrderList(t8) = [10, 20, 30, 40, 50, 60, 70, 80, 90]
--------------------------------------------------------

Homework Problem 3: Nested Frames

In this problem you will use iteration in to draw two-colored nested frame patterns like those shown below:

Each of the four patterns consists of concentric rectangular frames that have the same thickness and alternate between two colors. In the above example, each target has 10 nested frames, each of whose thicknesses is 1/20 of the dimensions allocated to the pattern.

In Picture World, such patterns can be drawn as a sequence of concentric filled rectangles, where the rectangles are draw from the outside in. You have been provided with the following method for creating a centered rectangular picture:

public Picture centeredRect (double fraction, Color c)
Returns a rectangle filled with color c that is centered in the picture canvas in which it is drawn. The width and height of the rectangle are each the given fraction of the enclosing picture canvas's width and height. The fraction argument must be between 0 and 1.

For example, using this method, here is a recursive implementation of the nested pattern:

public Picture nestedRec(int levels, double thickness, Color c1, Color c2) {
  if (levels == 0) {
    return empty();
  } else {
    return overlay(nestedRec(levels - 1, thickness, c2, c1),
                   centeredRect(levels*thickness, c1));
  }
}

Here, levels is the number of nested frames, thickness is the thickness of each frame edge, c1 is the outermost color, and c2 is the color that alternates with c1. The recursion accumulates a final picture that consists of levels centered rectangles overlayed on top of one another. Note how each level of the recursion decrements levels by 1 and swaps c1 and c2 (so that c2 is the outermost color in the nested subpicture). This strategy is not a tail recursive one, since there is still a pending overlay operation to be performed after the recursion returns.

In the rest of this problem, you will expore three iterative strategies for expressing the nested box pattern. You will be fleshing out the following skeletons in the file NestedFrames.java within the folder NestedFrames:

public Picture nestedIter(int n, double thickness, Color c1, Color c2) {
  // This method contains the initial call to nestedTail, which does all the work.
  return nestedTail(n, thickness, c1, c2, empty());
}
	
public Picture nestedTail(int n, double thickness, 
                          Color c1, Color c2, Picture ans) {
  // nestedTail should be a tail recursive method that returns a Picture 
  // that is the nested frames pattern. 

  // Replace the following stub by a correct definition.
  return empty();
}
	
public Picture nestedWhile(int n, double thickness, Color c1, Color c2) {
  // Use a while loop to accumulate and return a Picture 
  // that is the nested frames pattern.

  // Replace the following stub by a correct definition.
  return empty();
}
	
public Picture nestedFor(int n, double thickness, Color c1, Color c2) {
  // Use a for loop to accumulate and return a Picture 
  // that is the nested frames pattern.

  // Replace the following stub by a correct definition.
  return empty();
}

Your task is to flesh out all three methods so that they have the same behavior as nestedRec. You can test your methods by executing the NestedFrames.html applet. This will give you a window like that pictured at the beginning of this problem. By selecting an integer in the rightmost choice box, you can change the nesting level of the patterns. Your code does not have to take care of calculating the thickness; this calculation is already performed by the testing enviroment.

The patterns are arranged as follows inside the NestedFrames Applet window:

The upper left corner is the Picture generated by nestedRec().
The upper right corner is the Picture generated by nestedIter().
The lower left corner is the Picture generated by nestedWhile().
The lower right corner is the Picture generated by nestedFor().

In your definitions, pay attention to the following notes:

Recall that a Java while loop has the syntax

while (test-expression) {
  body-statements
}

and a Java for loop has the syntax

for (init-statement; test-expression; update-statement) {
  body-statements
}

A Java for loop is equivalent to the following while loop:

init-statement;
while (test-expression) {
  body-statements;
  update-statement;
}

The iterations are similar to the factorial and Fibonacci examples discussed in class, except that the result being accumulated is a Picture rather than a number.
Just as 1 is the identity value for multiplication and 0 is the identity value for addition, the empty picture is the identity value for the overlay operation.
Each of your iterations should decrement levels by 1. You should not decrement levels by 2!
In some of your definitions, you will find it helpful to introduce a "temporary variable" to hold a value that would otherwise be lost in a sequence of assignment statements. See the while loop version of the Fibonacci function defined in class for an example of an iteration that requires a temporary variable.
Each of your three definitions should be short (each can easily be defined in 10 lines or less). In this problem, there is no need to define any auxiliary methods.

Due: Tuesday, November 23 by 4:00 p.m.

This is the corrected version of problem set 8. The definitions of isBst, isInTree, and pathList have been changed and the base case for delete has been changed.

Reading Assignment:

About this Problem Set

How to turn in this Problem Set

Homework Problem 1: Making Change

Notes

Homework Problem 2: Binary Search Trees

Task 1: Drawing box-and-pointer diagram for insert

Task 2: Implementing delete

Task 3: Implementing inOrderList

Notes

Homework Problem 3: Nested Frames

This is the corrected version of problem set 8. The definitions of `isBst`, `isInTree`, and `pathList` have been changed and the base case for `delete` has been changed.

Task 1: Drawing box-and-pointer diagram for `insert`

Task 2: Implementing `delete`

Task 3: Implementing `inOrderList`