CS111, Wellesley College, Fall 2007

Problem Set 8

Due on Tuesday, November 13 at the start of class

About this Problem Set

The purpose of this problem set is to give you experience with iteration (while loops and for loops and tail recursion). In Tasks 1 and 2, you will write several iterative methods in PictureWorld and TurtleWorld, respectively. Task 3 is completely optional, and any points you earn for Task 3 will be added to your assignment grade as extra credit. In Task 3, you must evaluate which problem solving techniques that you have learned will be most useful to you in sorting a list of integers.

All code for this assignment is available in the ps08_programs folder in the cs111d download directory on the cs server.

How to turn in this Problem Set

You are required to turn in both a hardcopy and a softcopy. For general guidelines on problem set submission, including how to submit a softcopy and how to check if you softcopy submission was successful, click here. Please make sure to keep a copy of your work, either on a zip disk, or in your private directory (or, to play it safe, both).

Hardcopy Submission

Your hardcopy packet should consist of:
  1. The cover page;
  2. Your iteration table from Task 1a;
  3. Your modified NestedFrames.java file from Task 1b;
  4. Your modified StepWorld.java file from Tasks 2a and 2b;
  5. Your newly developed SortIntList.java file from Task 3, should you choose to solve this optional, extra-credit problem;
  6. Transcripts illustrating that your SortIntList application from Task 3 works correctly, should you choose to solve this optional, extra-credit problem.
Staple these together, and submit them at the start of class on the due date.

Softcopy Submission

You should submit your final version of your ps08_programs folder. In particular,

Task 1: Nested Frames

In this problem you will use iteration in to draw two-colored nested frame patterns like those shown below:

Each of the four patterns consists of concentric rectangular frames that have the same thickness, and alternate between two colors. In the above example, each target has 16 nested frames, each of whose thicknesses is 1/32 of the dimensions allocated to the pattern. (When the thickness is 1.0/(2*nestingLevels), the frames will evenly fill the alloted Picture space.)

In PictureWorld, each rectangular frame pattern can be drawn as a sequence of concentric filled rectangles, where the rectangles are draw from the outside in. You have been provided with the following method for creating a centered rectangular picture:

public Picture centeredRect (double fraction, Color c)
Returns a rectangle filled with color c that is centered in the picture canvas in which it is drawn. The width and height of the rectangle are each the given fraction of the enclosing picture canvas's width and height. The fraction argument must be between 0 and 1.

For example, using this method, here is a recursive implementation of the nested frame pattern:

public Picture nestedRec(int level, double thickness, Color c1, Color c2) {
     if (level == 0) {
          return empty();
     } else {
          return overlay(nestedRec(level - 1, thickness, c2, c1),
                         centeredRect(2*level*thickness, c1));
  }
}

Here, level is the number of nested frames, thickness represents the thickness of each frame edge as a fraction of the dimensions allocated to the pattern, c1 is the outermost color, and c2 is the color that alternates with c1. In the code that you are given, when nestedRec is initially invoked, the thickness argument is initially 1.0/(2 * initlevel), where initlevel is the initial level number. The nestedRec() method accumulates a final picture that consists of level centered rectangles overlayed on top of one another. Note how each level of the recursion decrements level by 1 and swaps c1 and c2 (so that c2 is the outermost color in the nested subpicture). This strategy is not a tail recursive one, since there is still a pending overlay() operation to be performed after the recursion returns.

In the rest of this problem, you will expore three iterative strategies for expressing the nested box pattern. You will start by creating an iteration table for the nested boxes.

Task 1a: Iteration Table

Create an iteration table for generating the nested frame picture with iteration. The table should have a column for each of the state variables in the iteration. These include the four parameters (level, thickness, c1, and c2) as well as a Picture variable that contains the "answer so far" for the current iteration state. You may also want to include an extra column that contains the picture that will be used in combination with the current answer to generate the next answer in the next row of the iteration table. This extra column should have pictures that can be created from the other state variables and the Picture methods that are available to you (including centeredRect()). Draw your iteration table for a process that produces the same picture as the following invocation, but does so in an iterative manner rather than a non-tail-recursive one: 

nestedRec(4,0.125,Color.blue,Color.green);
Turn this in with the hardcopy of your assignment.

Task 1b: Iterative Methods

For the rest of this problem, you will be fleshing out the NestedFrames class in the file NestedFrames.java in the folder NestedFrames in the ps08_programs folder. You are given the nestedRec() method above. You must write all the methods whose contracts appear below:
public Picture nestedIter(int n, double thickness, Color c1, Color c2)
This method contains the initial call to nestedTail(), which does all the work.

public Picture nestedTail(int n, double thickness, Color c1, Color c2, Picture ans)
A tail recursive method that returns a Picture that is the nested frames pattern.

public Picture nestedWhile(int n, double thickness, Color c1, Color c2)
Use a while loop to accumulate and return a Picture that is the nested frames pattern.

public Picture nestedFor(int n, double thickness, Color c1, Color c2)
Use a for loop to accumulate and return a Picture that is the nested frames pattern.

The nestedTail() (and therefore nestedIter()), nestedWhile(), and nestedFor() methods all yield the same picture as nestedRec, but do so via the corresponding iterative process, as described in your iteration table from Part a. The nestedAll Picture consists of four nested frames, where each of the four nested frames is generated by a different strategy:

You do not need to write or modify any code for the nestedAll Picture, other than filling in the four methods described above: nestedIter, nestedTail, nestedWhile, and nestedFor.

To experiment with a working version of a solution to this problem, run the applet NestedFrames in a web browser. Your solution should produce the same pictures as this sample solution applet.

Task 2: Turtle Steps

In this problem, you will use a turtle to draw sequences of steps made out of square blocks. For example:

The steps are controlled by two parameters:

Below, you are asked to implement two different strategies for drawing such steps. The skeleton code that you need to flesh out can be found in the StepMaker class within the StepWorld.java file within the folder StepWorld.

To experiment with a working version of a solution to this problem, run the applet StepWorld in a web browser. (Note: a "StepWorld" parameters window will appear at the top of your screen, but if you don't see it, it may be located behind your web browser window, so you should move your web browser window.) Your solution should produce the same drawings as this sample solution applet.

Task 2a: Row Decomposition

One way to decompose a set of steps is into rows of blocks. For instance, the sample steps above can be decomposed into five rows of blocks, where the first row consists of 5 blocks, the second row consists of 4 blocks, the third row consists of 3 blocks, the fourth row consists of two blocks, and the fifth row consists of 1 block.

In this part, you are to implement this strategy via the following three iterative methods:

public void block (int blockSize)
Use a for loop to draw a square block with the given block size. The turtle should return to its initial position and heading.

public void rowOfBlocks (int n, int blockSize)
Use a for loop to draw a row consisting of n blocks, each with size blockSize. The turtle should return to its initial position and heading.

public void stepsFor_1 (int n, int blockSize)
Use a for loop to draw set of steps consisting of n rows of blocks. The first row should contain n blocks, the second row should contain n-1 blocks, the third row should contain n-2 blocks, and so on. The final row should contain 1 block. The turtle should return to its initial position and heading.

You can test out your code for this part by (1) selecting stepFor_1 in the parameter window; (2) choosing values for n and blockSize in the parameter window; and (3) selecting Run in the Turtle window. The turtle originally starts at a coordinate of (0,0) (in the center of the screen) with a heading of 0 degrees (facing east). In order to test that stepsFor_1 properly returns the turtle to its initial position and heading, the testing code has the turtle turn left 225 degrees and move forward 100 steps after the call to stepsFor_1.

For example, the following parameter settings

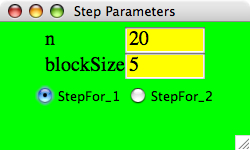
should result in the following picture:

Task 2b: Rectangle Decomposition

An alternative strategy for drawing the steps is based on the following observation: a set of steps with a base of n blocks can be drawn as the superposition of n rectangles whose widths increase from 1*blockSize to n*blockSize and whose heights decrease from n*blockSize to 1*blockSize. For example, the 5-block base steps shown below result from superimposing the five rectangles to its right so that their lower left points coincide:

Use this idea to implement the following method:

public void stepsFor_2 (int n, int blockSize)
Draw a set of steps with a base of n blocks, each of which is a block of size blockSize, and return the turtle to its initial position and heading. The problem should be decomposed into drawing n superimposed rectangles as described above. A for loop should be used to draw the rectangles. Keep in mind that you can accomplish this with only one for loop.

You may define auxiliary methods for this problem if you wish.

You can test out your code for this part as in part a, except you should select stepsFor_2 in the parameter window. To ensure that the turtle is returned to its initial position and heading, the testing code will draw the additional line extending from the lower left corner as mentioned in the testing notes for part a.

Task 3 (optional, extra-credit): An Application that Sorts a List of Integers

Task 3 is completely optional. You can receive a perfect score on this problem set without working on Task 3 at all. If you choose to work on Task 3, it will graded as any other problem set task, and any points that you earn will be awarded as extra credit. This problem set will be graded out of 50 points. Task 3 is woth up to 20 extra points. So you can receive up to 70 points on this 50 point assignment. If you have any questions about the optional, extra-credit nature of this task, please ask the instructors.

In this problem, you will write an appplication that takes a list of integers, and outputs a new list of integers consisting of the same integers from the original list, but in sorted order from least to greatest. For instance, if your application is given the list [8,121,-17,8,0,5] then your application should output the sorted list [-17,0,5,8,8,121].

You should start by creating a file named SortIntList.java that contains a class SortIntList, which extends the IntListOps class. Your SortIntList class should have a main method with the following formal parameter: String[] args. The main method should carry out the following steps:

Note: There are many different correct strategies for solving this problem. You should develop a strategy that you are comfortable with - we do not have a particular solution in mind. Regardless of which strategy you use to solve the problem, however, you should test your application on at least the test cases shown below. When you submit your assignment, you should include transcripts illustrating that your SortIntList application works correctly on cases you tested.

The figure below illustrates the execution of a working SortIntList application using the "Interactions" tab at the bottom of the Dr. Java window.