CS 111: Introduction to Recursion

Table of Contents

1. Reviewing Functions
2. First recursion: countDown
3. Gotcha-s in recursion
4. Exercise 1: Tower
5. Exercise 2: countUp
6. Exercise 3: countUpDown
7. Exercise 4: drawSquares
8. Bonus 1: bubbles
9. Bonus 2: fern

1. Reviewing Functions

Executing (running) the cell below doesn't do anything. Why?

def print_meta(s):
    print(s)
    print(s)

What should you do to be able to see something printed on the page? Do that on the cell below.

# Your code here
print_meta("boom")

boom
boom

Functions invoking other functions

Below there are three different cases all involving the same two functions: print_meta and print_metameta.
Without executing a cell try to guess what will be displayed (if anything) if the code is executed.
Then check your hypothesis.

Case 1: Ordered definitions, then invocation

Predict what will happen BEFORE you execute the cell

def print_meta(s):
    print(s)
    print(s)

def print_metameta(s):
    print_meta(s)
    print_meta(s)

print_metameta('foo')

foo
foo
foo
foo

Case 2: Unordered definitions, then invocation

Predict what will happen BEFORE you execute the cell

def print_metbmetb(s):
    print_metb(s)
    print_metb(s)

def print_metb(s):
    print(s)
    print(s)

print_metbmetb('foo')

foo
foo
foo
foo

Case 3: Unordered definitions, early invocation

Predict what will happen BEFORE you execute the cell

def print_metcmetc(s):
    print_metc(s)
    print_metc(s)

print_metcmetc('foo')

def print_metc(s):
    print(s)
    print(s)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-5-bad3a1028c1a> in <module>
      3     print_metc(s)
      4 
----> 5 print_metcmetc('foo')
      6 
      7 def print_metc(s):

<ipython-input-5-bad3a1028c1a> in print_metcmetc(s)
      1 def print_metcmetc(s):
----> 2     print_metc(s)
      3     print_metc(s)
      4 
      5 print_metcmetc('foo')

NameError: name 'print_metc' is not defined

2. First recursion: countDown

Execute the two cells below. Notice the repeated printing, despite the lack of an explicit for or while loop in the body of the function.

def countDown(n):
    '''Prints numbers from n down to 1''' 
    if n <= 0:  # Base case
        pass  # Do nothing
    else: # Recursive case: n>0: 
        print(n)
        countDown(n-1)

countDown(5)

5
4
3
2
1

Question: Try to predict what will be printed when running the next cell.

countDown(-5)

Side-note: simplifying the code by changing the base case

If the base case does nothing, we can re-write the conditional.

This is a general fact about if-statements, not necessarily related to recursion.

def countDown(n):
    '''Prints numbers from n down to 1''' 
    if n > 0:
        print(n)
        countDown(n-1)

countDown(6)

6
5
4
3
2
1

3. Gotcha-s in Recursion

Gotcha #1: Subproblem in not getting smaller

Below is an example of a common mistake when using recursion.

Can you figure out what is wrong in the code without running it?

def countDown(n):
    '''Prints numbers from n down to 1''' 
    if n <= 0:  # Base case
        pass  # Do nothing
    else: # Recursive case: n>0: 
        print(n)
        countDown(n)

countDown(10)

If you run the line above, you should see toward the end of the output, the dreaded error:

RuntimeError: maximum recursion depth exceeded while calling a Python object

It means that the memory allocated to your program doesn't have space anymore for all the function execution frames that are opened while your function is recursively invoking itself, endlessly!

Restart the kernel if you ran this code and got the error.

Gotcha #2: Missing the base case

The following example will also lead to infinite recursion. Can you explain why?
How can you fix the problem?

def countDown(n):
    '''Prints numbers from n down to 1''' 
    print(n)
    countDown(n-1)
        
countDown(10)

4. Exercise 1: Tower

Define a function tower that prints a tower using the characters of the input string name. The width of the tower should start with len(name) characters down to the last character.

tower('Wellesley') should print

Wellesley ellesley llesley lesley esley sley ley ey y

Hint: use string slicing.

def tower(name):
    """Prints a tower based on the string name from  
    all len(name) characters down to the last character"""
    # Your code here
    if len(name) == 0:
        return
    else:
        print(name)
        tower(name[1:]) # up to but not including last letter

tower("Wellesley")

Wellesley
ellesley
llesley
lesley
esley
sley
ley
ey
y

5. Exercise 2: countUp

Define the function countUp that counts up from 1 to n rather than n to 1. countUp(5) should print:

1  
2  
3  
4  
5

def countUp(n):
    '''Prints out integers from 1 up to n'''
    # Your code here
    if n > 0:
        countUp(n-1)
        print(n)

countUp(5)

1
2
3
4
5

6. Exercise 3: countDownUp

How about a function that counts down and up? This one is a bit more complex, but very elegant.

def countDownUp(n):
    """Prints integers from n down to 1
    and then from 1 up to n."""
    # Your code here
    if n > 0:
        print(n)
        countDownUp(n-1)
        print(n)

countDownUp(4)

4
3
2
1
1
2
3
4

7. Exercise 4: drawConcentricSquares

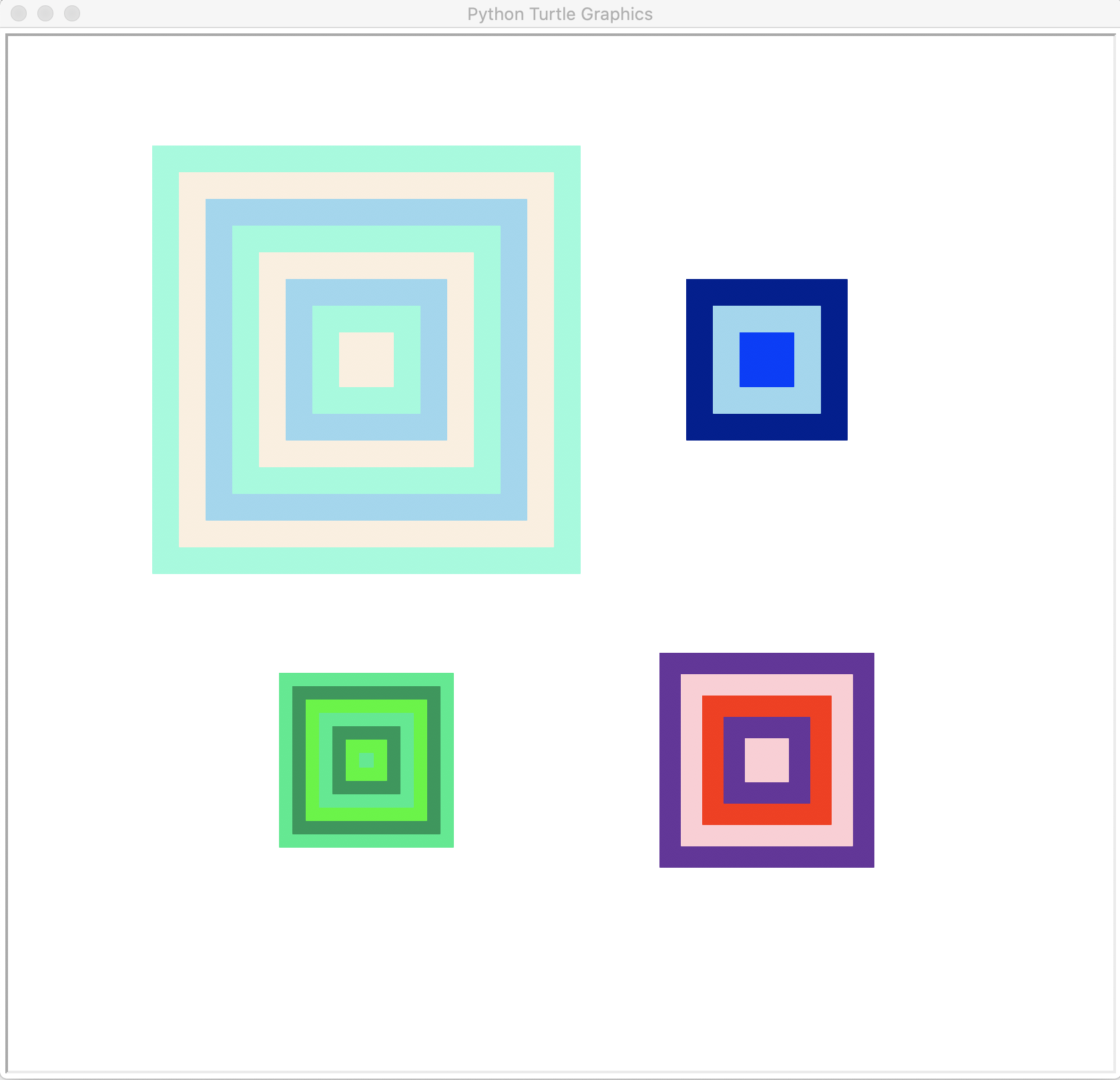
Here are some of images of examples of recursive squares.

Your Task

Flesh out the body of the recursive function below to draw one of the targets on the given canvas.

Hint: It is a short solution.

from turtle import *
from turtleBeads import *

def drawConcentricSquares(thickness, squareWidth, color1, color2, color3):
    '''
    Draws nested squares with alternating colors,
    color1, color2, and color3, where color1 is the outermost color. The
    thickness between each square is equidistant. squareWidth is the width 
    of the square.
    
    Hint: use drawSquare to draw the actual square
    '''
    # Your code here
    if squareWidth <= 0:
        pass
    else:
        color(color1)
        begin_fill()
        drawSquare(squareWidth)
        end_fill()
        drawConcentricSquares(thickness, squareWidth - thickness * 2, color2, color3, color1)
        

The above-shown image was produced by the following function calls:

reset()
noTrace()
teleport(-150, 150)
drawConcentricSquares(20, 320, 'Aquamarine', 'AntiqueWhite', 'skyblue')
teleport(150, 150)
drawConcentricSquares(20, 120, 'navyblue', 'skyblue', 'blue')
teleport(-150, -150)
drawConcentricSquares(10, 130, 'springgreen2', 'springgreen4', 'green')
teleport(150, -150)
drawConcentricSquares(16, 160, 'purple4', 'pink', 'red')
hideturtle()
showPicture()

8. Bonus Exercise 1: bubbles

This circle pattern is produced by a recursive function:

Below you can see how each part of the whole pattern is produced by calling the same function with slightly different arguments:

In the cell below, define your bubbles function as a recursive function. Make sure that you include a base case.

from turtle import *
from turtleBeads import *

def bubbles(size, minSize, color1, color2):
    """
    Draws a circle with two half-sized circles inside it, and two
    half-sized circles inside those, etc. unless the size is smaller than
    the given minimum, in which case nothing is drawn. The outer circle
    is colored color1, while the inner circles are color2, and their
    inner circles are color1 again, and so on.

    Hint: use the turtleBeads drawDot function for faster and smoother
    circles.
    """
    # Your code here
    if size < minSize:
        return
    else:
        color(color1)
        drawDot(size)
        leap(-size/4)
        bubbles(size/2, minSize, color2, color1)
        leap(size/2)
        bubbles(size/2, minSize, color2, color1)
        leap(-size/4)

reset()
noTrace()
bubbles(400, 12, 'MidnightBlue', 'LightSkyBlue')
showPicture()

9. Bonus Exercise 2: fern

Note: this is a harder exercise where you will have to be able to see the pattern and then trust your recursive calls. Besides recursion, your entire fern function will only move forward once and back once, and it will not use any loops.

This fern picture is produced by a recursive function:

Here you can see how the whole fern is produced by a single straight line, plus three smaller ferns, one to the left, one to the right, and one straight ahead:

Note: You will have to carefuly make sure that the turtle ends up exactly where it started after each recursive call. Do this by balancing calls to forward and back and any turning that you do throughout the function, without worrying about what the recursive calls do (because of course, they will not move the turtle, since that's the correct behavior).

from turtle import *
from turtleBeads import *

def fern(length, width):
    '''
    Draws a fern which is built from a single straight line and three
    smaller ferns: one continuing forward, and two more at 70-degree
    angles to either side. The length of the ferns on each side is
    half the initial width, while their widths are 1/7 of the initial
    length. The length of the fern directly in front has a length of 8/9th 
    of the initial length and 7/8 of the initial width.  The line drawn 
    is 1/8 of the initial length. Ferns where the length is less than 2 
    are not drawn.
    '''
    # Your code here
    if length < 2:
        return
    fd(length/8)
    lt(70)
    fern(width/2, length/7)
    rt(140)
    fern(width/2, length/7)
    lt(70)
    fern(length*8/9, width*7/8)
    penup()
    bk(length/8)
    pendown()

Here is how we can create the picture (it may take a few seconds to appear):

reset()
noTrace()
color("SpringGreen4")
penup()
lt(90)
bk(200)
pendown()
fern(400, 300)
showPicture()

Note: All the visualizations should have appeared in a separate Python window where Turtle drawings usually show. Search for that window on your list of open applications.