Lab 8

Our plan for today

Reminder: please fill out the PS6 feedback form if you haven't already.

To get started for today's lab, download the lab8_programs folder, rename it to include your name, and save all your python code into this folder. Create a new file called lab8.py. You will be writing many functions in this lab. Be sure to use lots of comments. You can also create new files, too, if you find that easier to manage.

recursive triangles
recursive box patterns (turtle graphics)
recursive box patterns (cs1graphics)
more recursive box patterns (cs1graphics)

You can use this function called asteriskLine(len) that creates a line of asterisks of length len.

  def asteriskLine(len):
      return '*' * len

Here are some examples of how asteriskLine() works:

Task 1a. Recursive triangles In this task, you will write a python function called asteriskTriangle() that will take a length parameter and draw a triangle pattern composed of lines of asterisks that get successively smaller with each line. The asteriskTriangle() function must be recursive.

You can use the given asteriskLine() function to create the lines in the triangular pattern.
Task 1b. Sideways Peaks Write a new function called peaks that takes two parameters:

height: the number of lines to the peak (and also the number of lines "descending" from the peak)
width: the number of asterisks in the initial line (increases by 3 per line until it reaches height number of lines).

Here are some sample invocations:

peaks(2,1)

<*
<****
****>
*>

peaks(4,2)

<**
<*****
<********
<***********
***********>
********>
*****>
**>

peaks(3,5)

<*****
<********
<***********
***********>
********>
*****>

peaks(1,0)

<
>

peaks(3,10)

<**********
<*************
<****************
****************>
*************>
**********>

peaks(8,1)

<*
<****
<*******
<**********
<*************
<****************
<*******************
<**********************
**********************>
*******************>
****************>
*************>
**********>
*******>
****>
*>

Your peaks function can use asteriskLines to produce the lines of asterisks (and string concatenate the "<" or ">" symbol as needed). Some hints:

the height parameter controls the number of lines printed. The total number of lines printed is always twice the height.
the width parameter tells how many asterisks are printed on the first (and last) lines. Each successive line of asterisks differs from its predecessor by exactly 3 asterisks.

Study this table to see the pattern:

peaks(4,2)

<**
<*****
<********
<***********
***********>
********>
*****>
**>

peaks(3,5)

<*****
<********
<***********
***********>
********>
*****>

peaks(2,8)

<********
<***********
***********>
********>

peaks(1,11)

<***********
***********>

peaks(0,13)

Click here for some notes that you might find helpful with respect to thinking about recursive problems Hint: print statements can be really helpful both for understanding how your function works and also for debugging your code. Task 2. Recursive boxes with turtle graphics In the lab8_programs folder, open the file called recursiveTurtle.py. Note the initialize_turtle() function that gets the turtle and screen in good initial position, color, speed, etc. Note also how the run() function calls initialize_turtle(). Eventually, the call to your function (e.g., row()) will go inside run(). Then to test your code, follow these steps:

run your file in Canopy
type run() in the interactive pane
watch your turtle do its thing

In this task, you will choose one of the versions of the square() function below. Note that Version A square() uses a for loop and is not recursive. In most of the screen shots that are shown below, the turtle's pen was set to red with this line of code: pencolor('red').

# Version A: Uses a for loop
def square(length):
    """draws a square of size length maintains heading 
       and position invariant"""
    for i in range(1,5): # or for i in range(4)
        fd(length)
        lt(90)

# Version B: No loops
def square(length):
    """draws a square of size length maintains heading 
       and position invariant"""
        fd(length)
        lt(90)
        fd(length)
        lt(90)
        fd(length)
        lt(90)
        fd(length) # back to starting location
        lt(90)  # heading in same direction as start

Task 2a: row(number, size) Write a recursive method called row(number,size) that draws a horizontal row of number boxes of size size. This function must be recursive and maintain a position and heading invariant.

row(3,50)

row(5,25)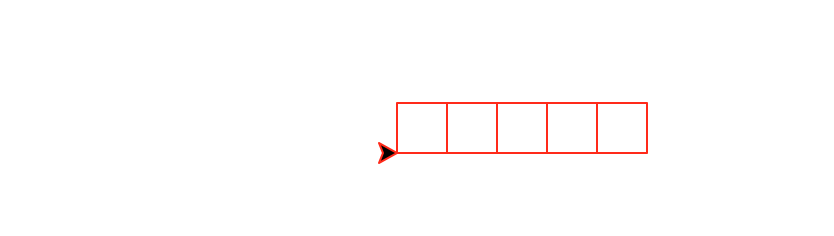

Task 2b: spacedRow(number,size) Write a recursive method called spacedRow(number,size) that draws a horizontal row of number boxes of size size with a constant space of size/4 between each square. This function must be recursive and maintain a position and heading invariant.

spacedRow(3,50)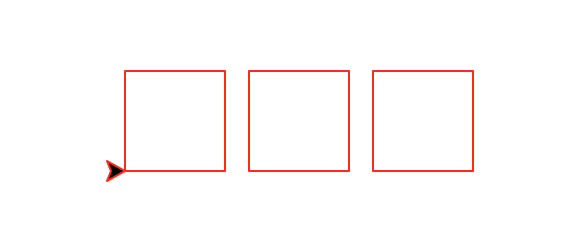

spacedRow(5,25)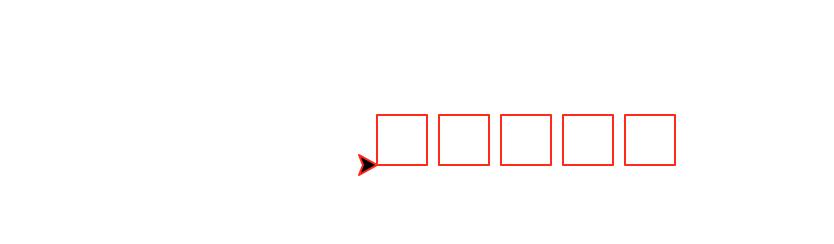

Task 2c: decreasingRow(number,size) Write a recursive method called decreasingRow(number,size) that draws a horizontal row of number boxes. The first box has size size and each subsequent box is half the size of the previous one. This function must be recursive and maintain a position and heading invariant.

decreasingRow(3,100)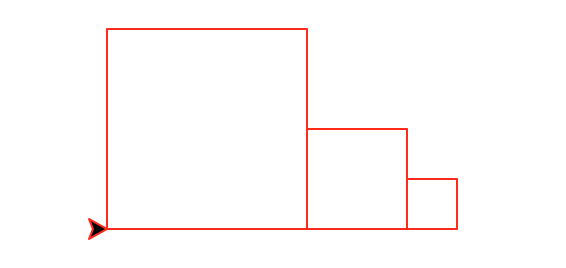

decreasingRow(5,100)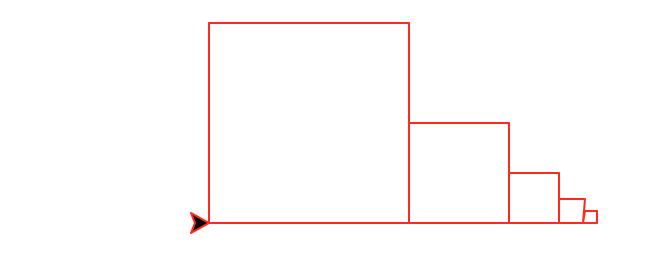

Task 2d: nestedSquares(number,size) Write a recursive method called nestedSquares(number,size) that draws number nested squares. The largest square has size size and each subsequent box is half the size of the previous one. The boxes are anchored in the lower left corner. This function must be recursive and maintain a position and heading invariant.

nestedSquares(3,90)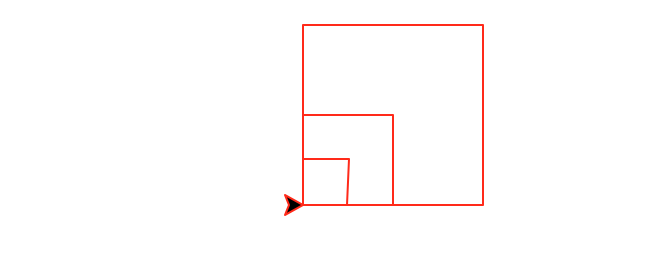

nestedSquares(5,130)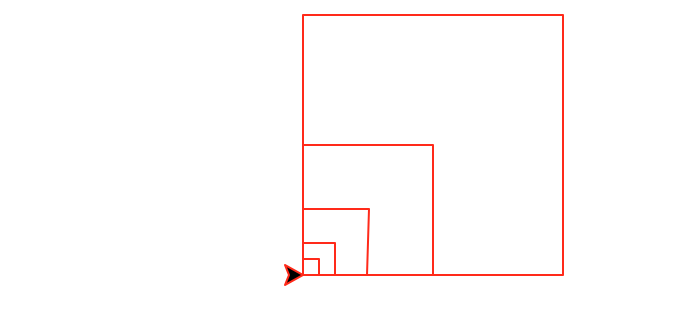

Task 2e: diagonal(number,size) Write a recursive method called diagonal(number,size) that draws number decreasing diagonal squares. The largest square has size size and each subsequent square is half the size of the previous one. This function must be recursive and maintain a position and heading invariant.

diagonal(1,100)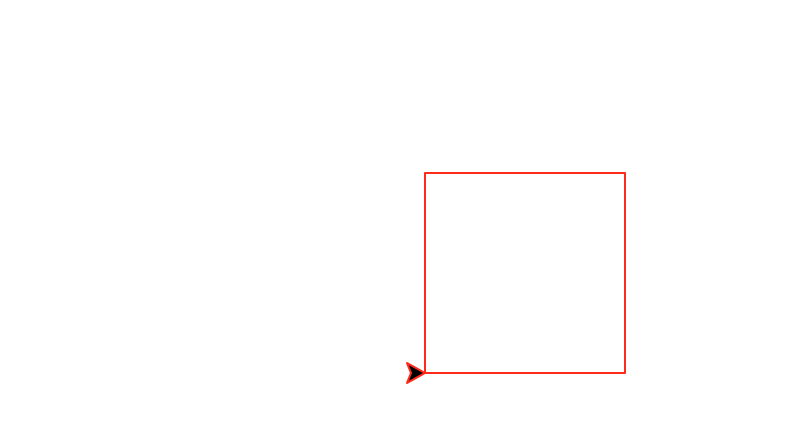

diagonal(2,100)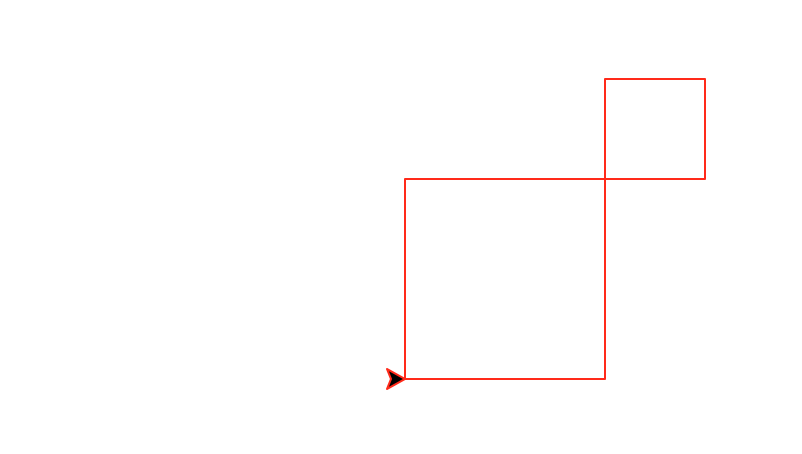

diagonal(3,100)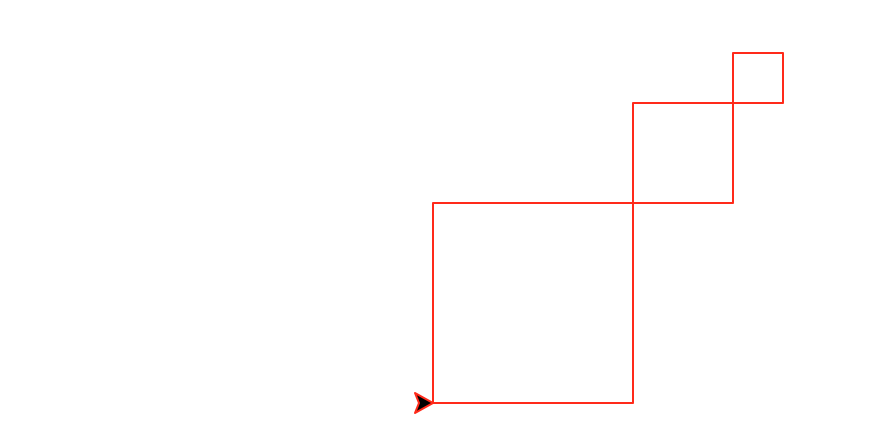

Task 2f: superDiagonal(number,size) Write a recursive method called superDiagonal(number,size) that draws number decreasing diagonal squares. The largest square has size size and each subsequent square is half the size of the previous one. In superDiagonal, squares are placed on the diagonal at both the upper right corner and the lower left corner. This function must be recursive and maintain a position and heading invariant.

`superDiagonal(1,125)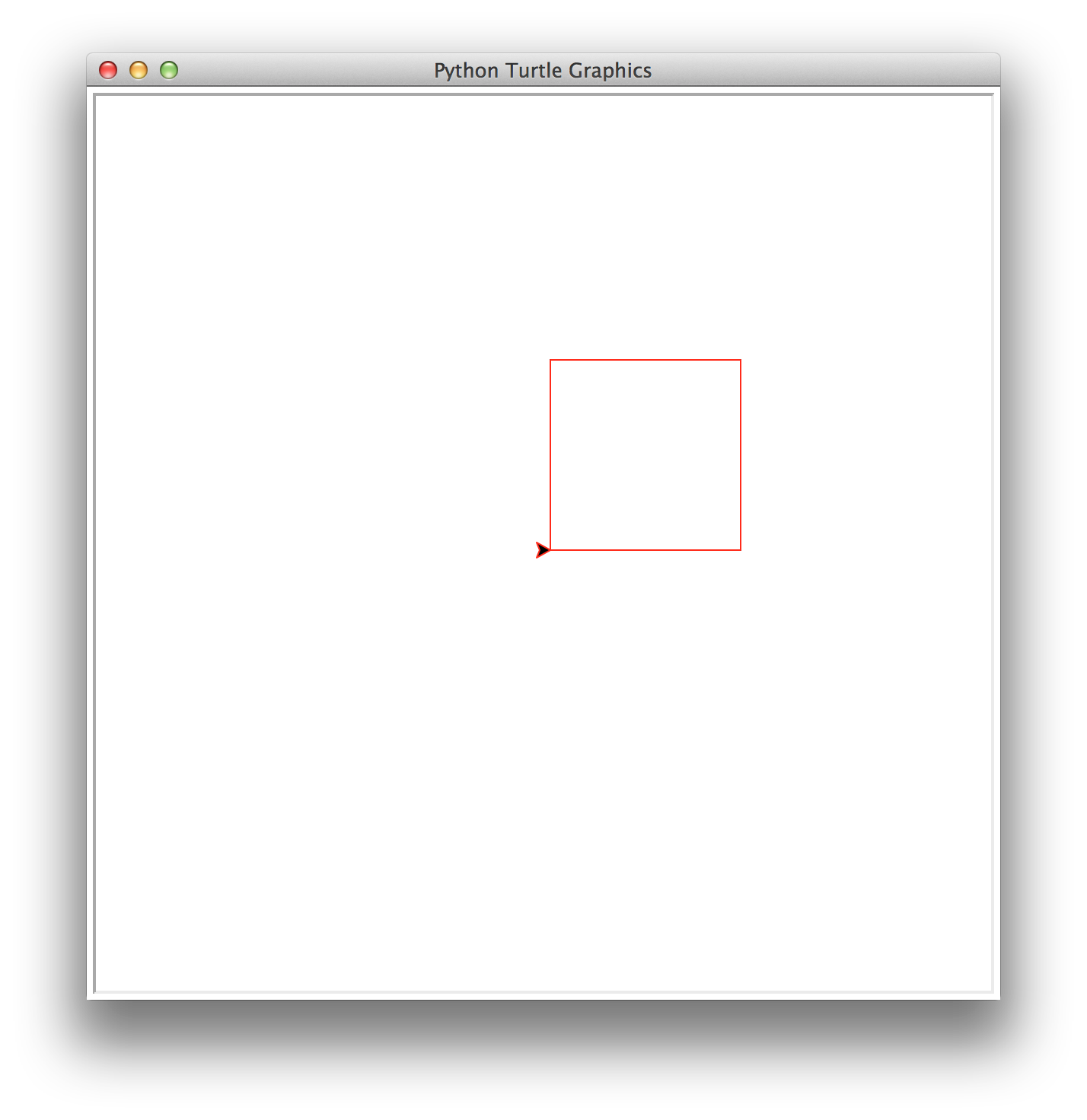`	`superDiagonal(2,125)`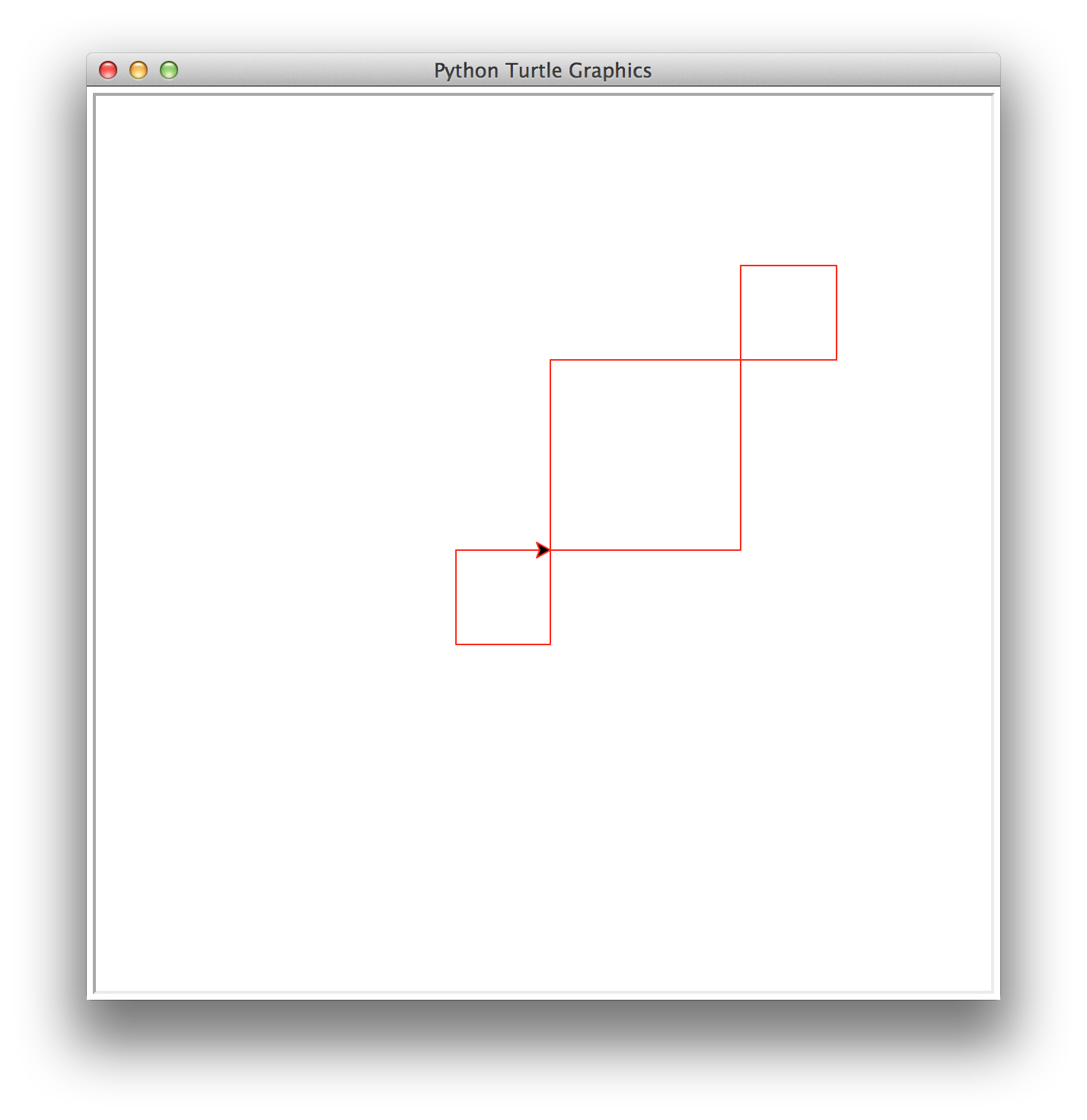
`superDiagonal(3,125)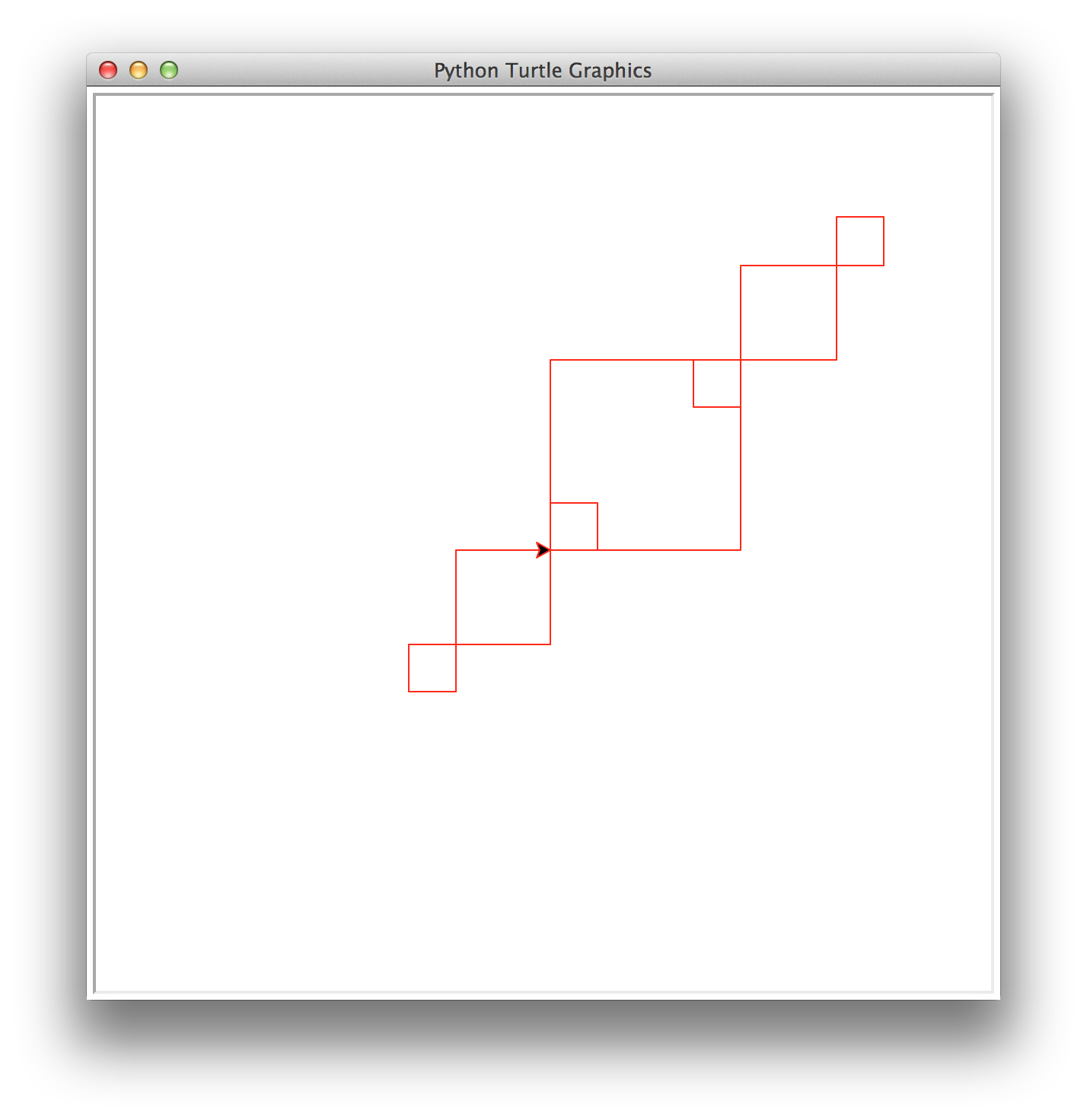`	`superDiagonal(4,125)`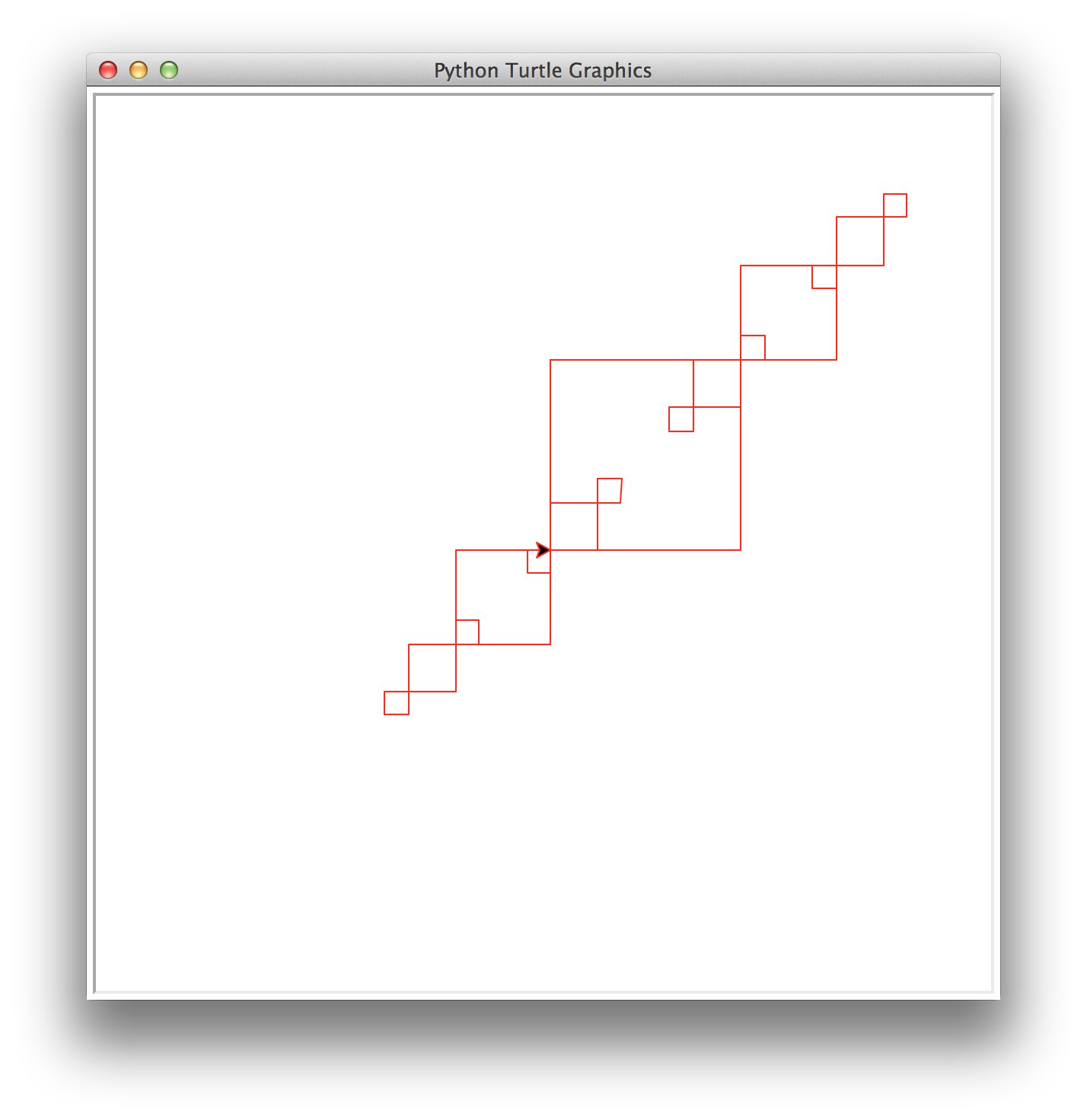

Task 3. Recursive pictures using cs1graphics: nested boxes For this task, we are providing the box(x,y,size,color1,canvas) that draws a single box of side length size, centered at (x,y), filled with the color color1, drawn on the given canvas.

def box(x,y,size,color1,canvas):
    b = Rectangle(size,size,Point(x,y))
    b.setFillColor(color1)
    canvas.add(b)

Here are some sample invocations of the box function. Before invoking box, this code is executed to set up the canvas:


labcanvas = Canvas(500,500,'ivory','labcanvas')

Your task is to write a recursive function called makeNestedBoxes(x,y,size,color1,color2,canvas) that produces nested boxes of alternating colors. The largest box is drawn first, filled with color1, and then the next box has a side length that is 10 smaller and is filled with color2, etc. This alternating pattern continues until the box has a size that is less than 10. Your makeNestedBoxes() function must be recursive.

Invocations to create the boxes above are as follows:


# first, create and name the canvas
paper = Canvas(500,500,'darkolivegreen')

# makeNestedBoxes(x,y,size,color1,color2,paper)

makeNestedBoxes(200,400,100,'red','ivory',paper)
makeNestedBoxes(150,100,200,'purple','gold',paper)
makeNestedBoxes(400,200,180,'navy','lightskyblue',paper)

Task 4. Recursive pictures using cs1graphics: box pattern Building upon the makeNestedBoxes() function above, this task adds smaller versions of nested boxes at each of the four corners of every box. The ratio of a box size to the corner box size is 1:3. The corner boxes can only be drawn when they have a size greater than or equal to 10. Your nestedBoxPattern() function must be recursive. Hint: start with only one corner box (e.g. upper left), and when that works, go back and add in the other 3 corner boxes..

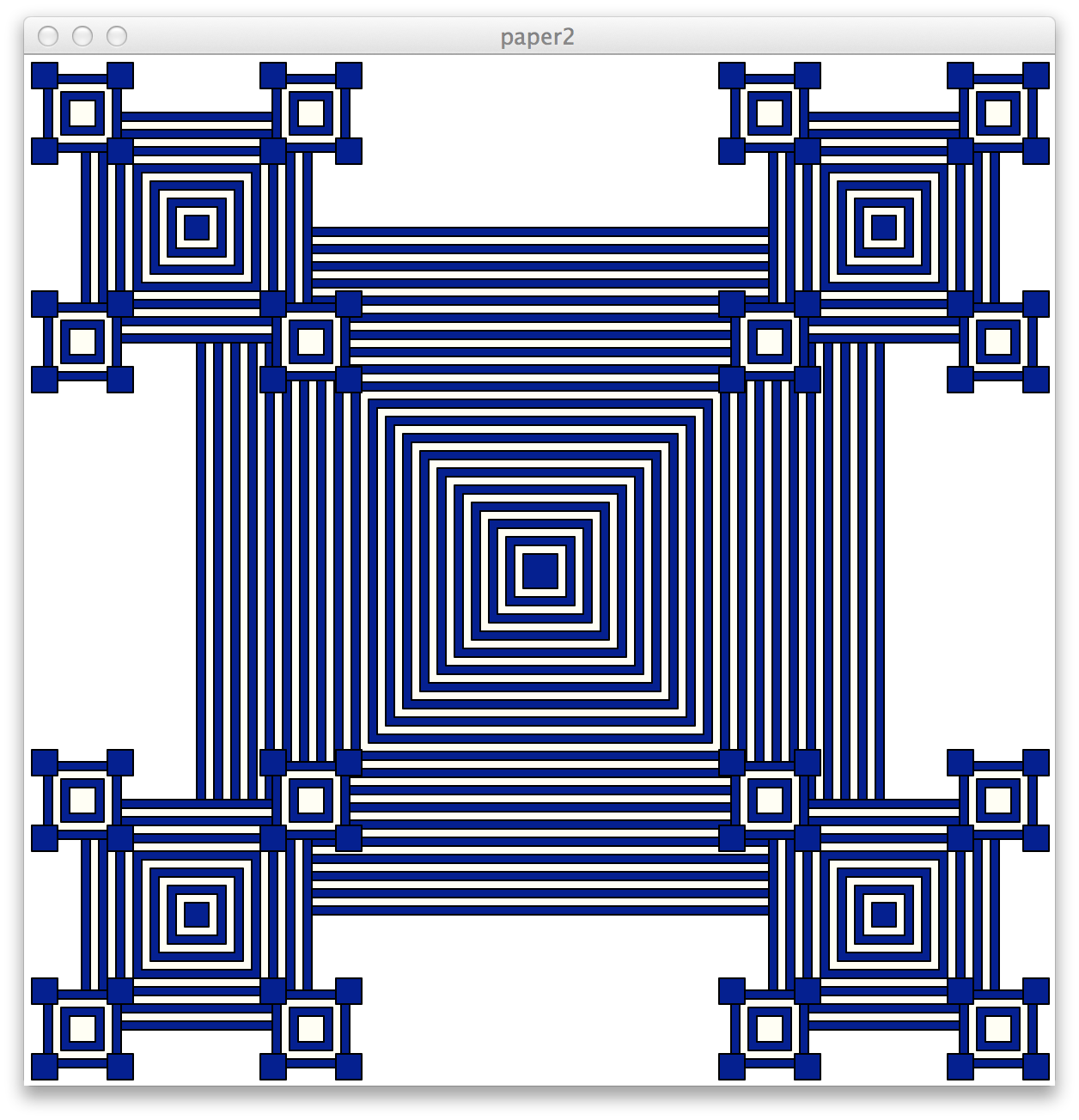
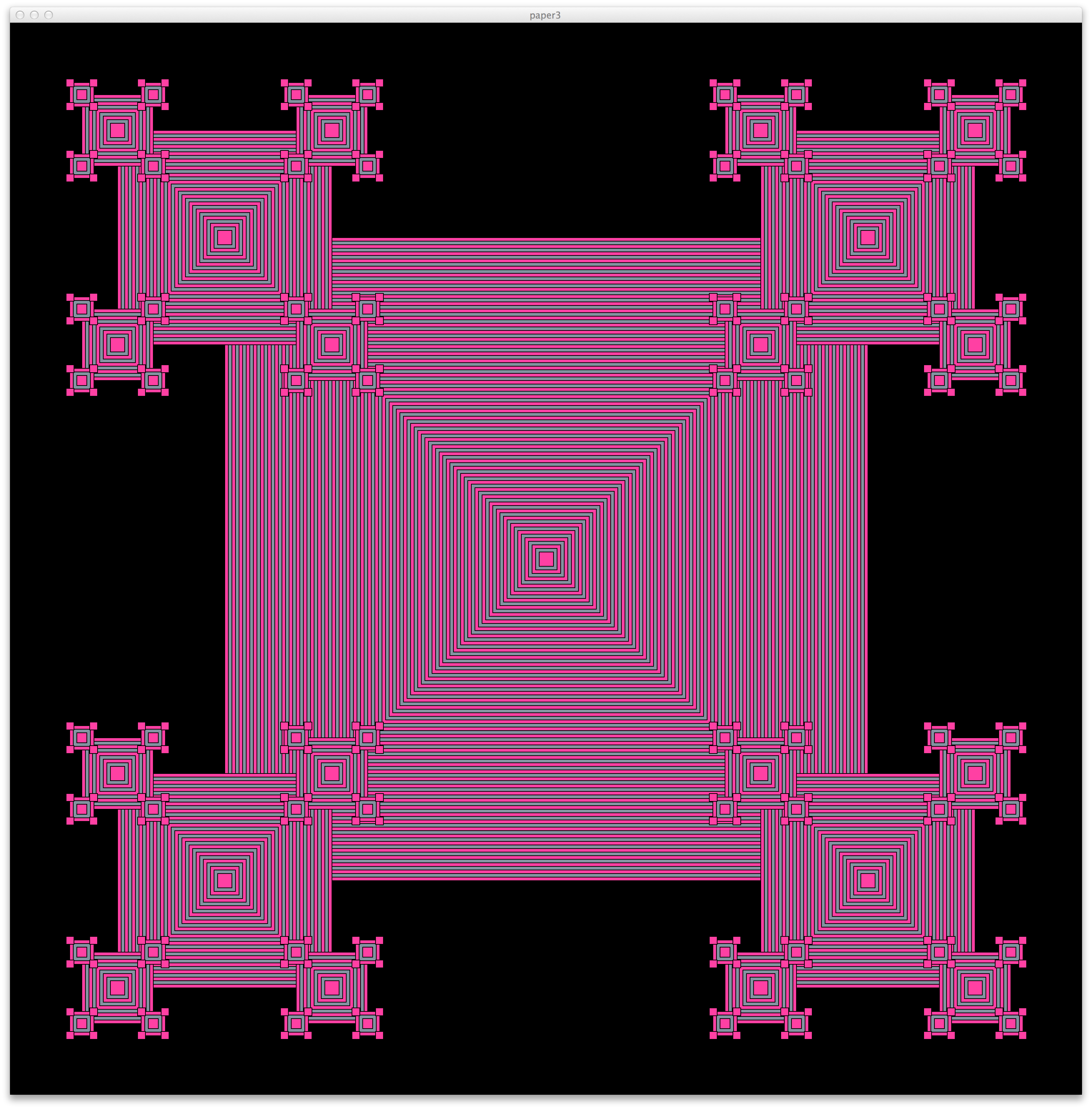
The patterns above were generated by the following code:

paper2 = Canvas(600,600,'white','paper2')
nestedBoxPattern(300,300,400,'navy','ivory',paper2)

and

paper3 = Canvas(1500,1500,'black,'paper3')
nestedBoxPattern(750,750,500,'deeppink','slategray',paper3)

nestedBoxPattern() takes 6 parameters: the x and y point where the box is centered, the size of the largest box, the outermost color1, the alternating color2, and the canvas where the drawing should appear. Note: here is a chart of the colors available to you through cs1graphics.py.

Lab 8.

Our plan for today