Lab 6

Today

• Writing recursive methods (in BuggleWorld, and in a JAVA application)
• A Recursive JEM

Download the lab6_programs folder from the cs111d account on cs.wellesley.edu. For the following tasks, write your recursive methods and add testing code in the BagelWorldRec.java file that is provided for you, in lab6_programs.

Note that the tasks today might be challenging for many people. Try as many as you have time during the lab, and don't be disappointed if you don't get to all of them. However, make sure you get back to it, study and understand the solutions once they are posted (some time late on Wednesday.) Tasks 3 and on can be worked on in any order. Just choose what is more appealing to you.

The Console window

You are advised to add System.out.println() statements to the recursive methods that you will be writing. These statements, when thoughtfully placed, can help you understand how your program works, and can be a big help in debugging when your program doesn't work, or doesn't work correctly. Each time a
System.out.println("message");
statement is reached, the "message" is printed in the console window in DrJava. Remember to examine the console as you run, or step through your program, and clear it between program runs (in DrJava: Tools → Clear Console).

The size of the grid

In some of the problems today, you may need a bigger or smaller grid. Use the BuggleWorld method setDimensions(), in the setup() method, to set the size of the grid. Locate and check the BuggleWorld contract, in the CS111 web site.

Testing your methods

Call each method you write in the BagelWorldRec class from the run(). Test your methods a few times, with different arguments each time, to make sure they work fine.

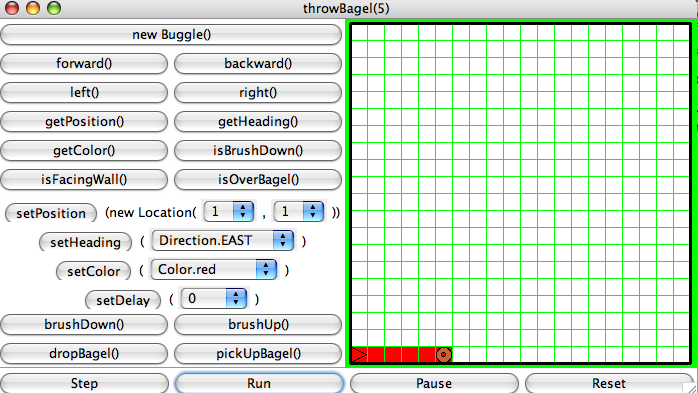
Task 1 — throwBagel()

Write a recursive method, throwBagel(), that places a bagel a number of cells forward from the buggle's position. The number of cells forward is passed as a parameter to the method. The position and heading of the buggle should not change after the method has been invoked. The cells between the buggle's starting position and the bagel's position will be colored the same color as the buggle's color.
Here is a snapshot of invoking the throwBagel() method:

Task 2 — JEM Diagrams for Recursive methods

Draw a Java Execution Model diagram that shows all of the execution frames created by invoking the following run() method on an instance of the BagelWorldRec:

  public void run() {
    BagelBuggleRec betty = new BagelBuggleRec();
    
    betty.throwBagel(3);
    
  } 

Your diagram should depict the point in time when the invocation of run() returns. Although Java can discard an execution frame when control returns from it, you should not discard any frames when drawing your diagram.

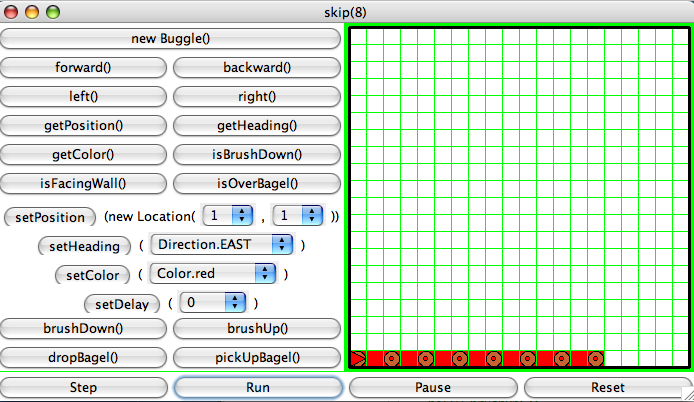
Task 3 — skip()

Write a recursive method, skip(), that produces a row of bagels in every other cell on a grid. The method takes one integer parameter, n, that is the number of bagels that are dropped in the row. The position and heading of the buggle are not changed after the invocation of the method. Write all your code within the skip() method (no auxiliary methods used), and do not use the paintCell() method. You can assume there is enough space on the grid for all the bagels to be placed. Here is a snapshot of invoking the skip() method:

Task 4 — JAVA application: Factorials

This is a typical example of recursion in math. The value refered to as N! is defined for any positive integer as the product of all integers beween 1 and N inclusive. Therefore,

3! = 3*2*1 = 6, and

5! = 5*$*3*2*1 = 120.

Express the above formula recursively, and write a JAVA application, named Factorials to compute, and print out factorials.

Task 5 — triangle()

Write a recursive method, triangle() that produces a triangle of bagels, as shown below:

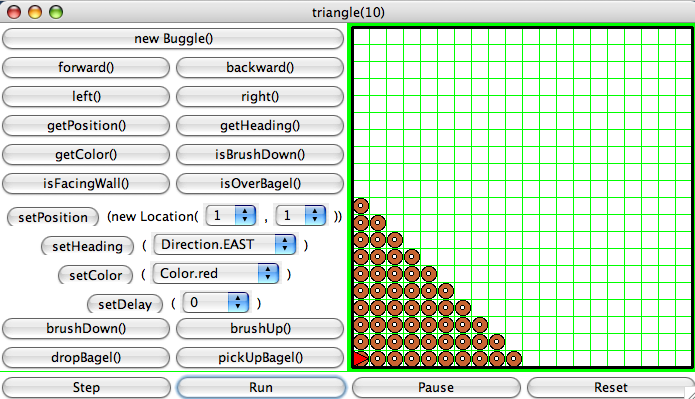
Of course, the size of the base of the triangle should be flexible.

Task 6 — spiral()

Write a recursive method, spiral() that produces a spiral of bagels, as shown below:

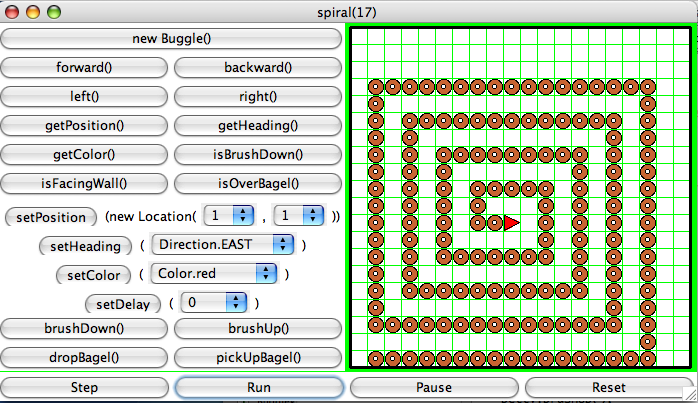
The size of the outside spiral should be flexible. Notice that you get better-looking spiral in the center when the size of the side of the biggest spiral is a power of 2 + 1 (i.e. size of side of biggest spiral = 2ⁿ + 1). Consider this when you are testing your method.